题目内容
16.已知α、β是一元二次方程x2-2x-3=0的两个根,则α+β的值是( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
分析 根据根与系数的关系得到α+β=-$\frac{b}{a}$=2,即可得出答案.
解答 解:∵α、β是一元二次方程x2-2x-3=0的两个根,
∴α+β=-$\frac{b}{a}$=2;
故选A.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )
如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )
 如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )
如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |
11.计算:-1-2=( )
| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
1.若函数y=mx2-(m-3)x-4的图象与x轴只有一个交点,则m的值为( )
| A. | 0 | B. | 1或9 | C. | -1或-9 | D. | 0或-1或-9 |
5.下列四个多项式,能因式分解的是( )
| A. | a-1 | B. | a2+1 | C. | x2-4y | D. | x2-6x+9 |
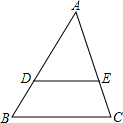 在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
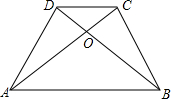 如图,已知在梯形ABCD中,AB∥CD,且AB=3CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么$\overrightarrow{AO}$$\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
如图,已知在梯形ABCD中,AB∥CD,且AB=3CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么$\overrightarrow{AO}$$\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)