题目内容
11.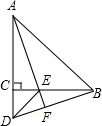 如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.
如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.
分析 根据SAS推出△ACE≌△BCD,得到对应边相等AE=BD.
解答 答:AE=BD,
证明:∵△ABC、△ECD都是等腰直角三角形,
∴AC=BC,CE=CD,∠ACE=∠BCD=90°,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD=90°}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴AE=BD.
点评 本题考查了全等三角形的性质和判定,等腰直角三角形的性质的应用,解此题的关键是推出△ACE≌△BCD,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
1.若函数y=mx2-(m-3)x-4的图象与x轴只有一个交点,则m的值为( )
| A. | 0 | B. | 1或9 | C. | -1或-9 | D. | 0或-1或-9 |
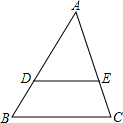 在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.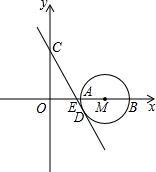 如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A,B.已知抛物线$y=\frac{1}{6}{x^2}+bx+c$过点A和B,与y轴交于点C.
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A,B.已知抛物线$y=\frac{1}{6}{x^2}+bx+c$过点A和B,与y轴交于点C.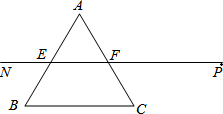 射线PN与等边△ABC的两边AB,BC分别交于点E,F,且BC∥EF,AE=BE=2cm,PF=4cm.动点Q从点P出发,沿射线PN以每秒2cm的速度向左移动,同时△ABC也沿射线PN以每秒1cm的速度向左移动,经过t秒,以点Q为圆心,$\sqrt{3}$cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=2或3≤t≤7或t=8.(单位:秒)
射线PN与等边△ABC的两边AB,BC分别交于点E,F,且BC∥EF,AE=BE=2cm,PF=4cm.动点Q从点P出发,沿射线PN以每秒2cm的速度向左移动,同时△ABC也沿射线PN以每秒1cm的速度向左移动,经过t秒,以点Q为圆心,$\sqrt{3}$cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=2或3≤t≤7或t=8.(单位:秒)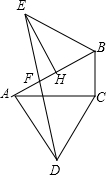 已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF.