题目内容
19.在△ABC中,∠C=90°,BC=6,sinA=$\frac{3}{5}$,求AC、AB的值.分析 首先由正弦函数的定义可知:$\frac{BC}{AB}=\frac{3}{5}$,从而可求得AB的长,然后由勾股定理可求得BC的长.
解答 解:如图所示:
∵sin∠A=$\frac{BC}{AB}=\frac{3}{5}$,
∴$\frac{6}{AB}=\frac{3}{5}$.
∴AB=10.
由勾股定理得:AC=$\sqrt{A{B}^{2}-C{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8.
点评 本题主要考查的是解直角三角形,掌握勾股定理和正弦函数的定义是解题的关键.

练习册系列答案
相关题目
7.下列说法中,正确的个数为( )
①对于任何有理数m,都有m2>0;
②对于任何有理数m,都有m2=(-m)2;
③对于任何有理数m,n(m≠n),都有(m-n)2>0;
④对于任何有理数m,都有m3=(-m)3.
①对于任何有理数m,都有m2>0;
②对于任何有理数m,都有m2=(-m)2;
③对于任何有理数m,n(m≠n),都有(m-n)2>0;
④对于任何有理数m,都有m3=(-m)3.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
8.若1<x<2,则$\sqrt{{(x-3)}^{2}}$+$\sqrt{{(x-1)}^{2}}$的值为( )
| A. | 2x-4 | B. | -2 | C. | 4-2x | D. | 2 |
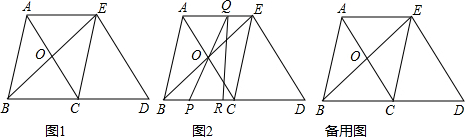
 如图,Rt△ABC中,AB=AC,∠A=90°,∠B的平分线交AC于D,从C点向BD的延长线作垂线,垂足为E.求证:BD=2CE.
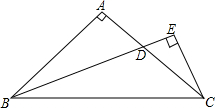
如图,Rt△ABC中,AB=AC,∠A=90°,∠B的平分线交AC于D,从C点向BD的延长线作垂线,垂足为E.求证:BD=2CE.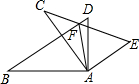 已知,如图,AB⊥AD,AC⊥AE,AB=AC,AD=AE.求证:
已知,如图,AB⊥AD,AC⊥AE,AB=AC,AD=AE.求证: 已知AD是BC边上的中线,AF=2FD,求证:AE=EC.
已知AD是BC边上的中线,AF=2FD,求证:AE=EC.