题目内容
9.在(-$\sqrt{2}$)0,$\root{3}{8}$,0,$\sqrt{9}$,$\root{3}{4}$,0.010010001…,-$\frac{π}{2}$,-0.666…,$\sqrt{5}$,3.1415,2.010101…,2-$\sqrt{3}$ (相邻两个1之间有1个0)中,无理数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.
解答 解:在(-$\sqrt{2}$)0,$\root{3}{8}$,0,$\sqrt{9}$,$\root{3}{4}$,0.010010001…,-$\frac{π}{2}$,-0.666…,$\sqrt{5}$,3.1415,2.010101…,2-$\sqrt{3}$ (相邻两个1之间有1个0)中,无理数有:$\root{3}{4}$,0.010010001…,-$\frac{π}{2}$,$\sqrt{5}$,2.010101…(相邻两个1之间有1个0),2-$\sqrt{3}$,共6个,
故选D.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
14.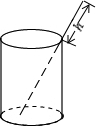 将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
 将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )| A. | h≤17 | B. | 7≤h≤16 | C. | 15≤h≤16 | D. | h≥8 |
 已知:一次函数y=2x-4
已知:一次函数y=2x-4