题目内容
10.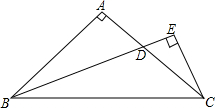 如图,Rt△ABC中,AB=AC,∠A=90°,∠B的平分线交AC于D,从C点向BD的延长线作垂线,垂足为E.求证:BD=2CE.
如图,Rt△ABC中,AB=AC,∠A=90°,∠B的平分线交AC于D,从C点向BD的延长线作垂线,垂足为E.求证:BD=2CE.
分析 分别延长BA,CE交于点F,根据已知条件,易证△BFE≌△BCE,所以BF=BC,所以∠F=∠BCE,根据等腰三角形三线合一这一性质可得CE=FE,再证明△ABD≌△ACF,证得BD=CF,从而证得BD=2CE.
解答 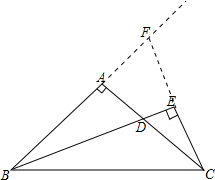 证明:分别延长BA,CE交于点F,
证明:分别延长BA,CE交于点F,
明:∵∠ABC的平分线交AC于D,
∴∠FBE=∠CBE,
∵BE⊥CF,
∴∠BEF=∠BEC,
在△BFE和△BCE中
$\left\{\begin{array}{l}{∠FBE=∠CBE}\\{BE=BE}\\{∠BEF=∠BEC}\end{array}\right.$,
∴△BFE≌△BCE(ASA),
∴CE=EF,
∴CF=2CE,
∵∠BAC=90°,且AB=AC,
∴∠FAC=∠BAC=90°,∠ABC=∠ACB=45°,
∴∠FBE=∠CBE=22.5°,
∴∠F=∠ADB=67.5°,
又AB=AC,
在△ABD和△ACF中,
$\left\{\begin{array}{l}{∠F=∠ADB}\\{∠FAC=∠BAD}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACF(AAS),
∴BD=CF,
∴BD=2CE.
点评 本题考查了全等三角形的判定和性质以及等腰三角形的性质,解题的关键是熟练应用等边对等角以及等腰三角形三线合一的性质.

练习册系列答案
相关题目
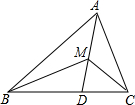 已知:AB>AC,AD为∠BAC的角平分线,M为AD上任一点,求证:BM-CM<AB-AC.
已知:AB>AC,AD为∠BAC的角平分线,M为AD上任一点,求证:BM-CM<AB-AC.
 如图,AD是△ABC的高,点E在AC上,且EG⊥BC于G,∠1=∠2,∠3=58°,∠C=35°,求∠BAC的度数.
如图,AD是△ABC的高,点E在AC上,且EG⊥BC于G,∠1=∠2,∠3=58°,∠C=35°,求∠BAC的度数.