题目内容
1.填上适当的数,使等式成立:x2-5x+(-$\frac{5}{2}$)2=(x-$\frac{5}{2}$)2;x2+3x+($\frac{3}{2}$)2=(x+$\frac{3}{2}$)2.
分析 根据完全平方公式可知左边加上一次项系数一半的平方即可利用完全平方公式分解因式.
解答 解:x2-5x+(-$\frac{5}{2}$)2=(x-$\frac{5}{2}$)2;x2+3x+($\frac{3}{2}$)2=(x+$\frac{3}{2}$)2.
故答案是:(-$\frac{5}{2}$)2;-$\frac{5}{2}$;($\frac{3}{2}$)2;$\frac{3}{2}$.
点评 此题考查配方法的运用,掌握所配常数项是二次项系数一半的平方是解决问题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
6.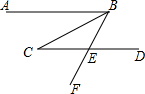 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠CEF的度数是( )| A. | 16° | B. | 33° | C. | 49° | D. | 66° |
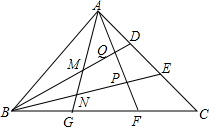 △ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.
△ABC面积为S,AD=DE=EC,BG=GF=FC,AG,AF与BD,BE分别交于M,N,P,Q,连接EF.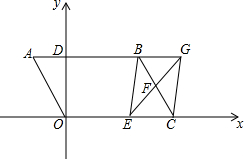 如图,平行四边形OABC中,OA=2$\sqrt{3}$,∠A=60°,AB交y轴于点D,点C(3$\sqrt{3}$,0),F是BC的中点,E在OC上从O向C移动,EF的延长线与AB的延长线交于点G.
如图,平行四边形OABC中,OA=2$\sqrt{3}$,∠A=60°,AB交y轴于点D,点C(3$\sqrt{3}$,0),F是BC的中点,E在OC上从O向C移动,EF的延长线与AB的延长线交于点G.