题目内容
10.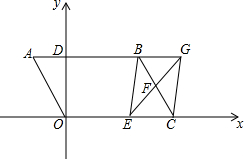 如图,平行四边形OABC中,OA=2$\sqrt{3}$,∠A=60°,AB交y轴于点D,点C(3$\sqrt{3}$,0),F是BC的中点,E在OC上从O向C移动,EF的延长线与AB的延长线交于点G.
如图,平行四边形OABC中,OA=2$\sqrt{3}$,∠A=60°,AB交y轴于点D,点C(3$\sqrt{3}$,0),F是BC的中点,E在OC上从O向C移动,EF的延长线与AB的延长线交于点G.(l)求D、B的坐标;
(2)求证:四边形ECGB是平行四边形;
(3)求当OE是多少时,四边形ECGB是矩形;OE是多少时,四边形ECGB是菱形.
(4)设OE=x,四边形OAGC的面积为y,请写出y与x的关系式.
分析 (1)由含30°直角三角形的性质可得AD=$\sqrt{3}$,由锐角三角函数易得OD的长,可得D点坐标,由平行四边形的性质可得AB的长,易得BD的长,可得B点坐标;
(2)由平行四边形的性质可得AG∥OC,∠BGE=∠GEC,由F是CB的中点,易证得△BFG≌△CFE,由全等三角形的性质可得BG=CE,由平行四边形的判定定理,一组对边平行且相等的四边形是平行四边形,证得结论;
(3)由矩形的性质可得∠BEC=90°,又因为∠A=∠BCE=60°,易得∠EBC=30°,可得EC的长,求得OE的长;由菱形的性质可得△BEC是等边三角形,易得EC的长,求得OE;
(4)由OE=x,可得BG=CE=3$\sqrt{3}$-x,利用平行四边形和三角形的面积公式可得四边形OAGC的面积,得y与x的关系式.
解答 (1)解:∵平行四边形OABC中,∠A=60°,
∴∠ADO=90°,∠AOD=30°,
∵OA=2$\sqrt{3}$,
∴AD=$\sqrt{3}$,OD=3,
∴D坐标(0,3),
∵AB=OC=3$\sqrt{3}$,
∴BD=AB-AD=3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$,
∴B坐标(2$\sqrt{3}$,3);
(2)证明:∵四边形OABC是平行四边形,
∴AG∥OC,
∴∠BGE=∠GEC,
∵F是CB的中点,
∴BF=CF,
又∵∠BFG=∠CFE,
在△BFG与△CFE中,
$\left\{\begin{array}{l}{∠BGE=∠GEC}\\{BF=CF}\\{∠BFG=∠CFE}\end{array}\right.$,
∴△BFG≌△CFE(ASA),
∴BG=CE,
∴四边形ECGB是平行四边形;
(3)解:∵四边形ECGB是矩形,
∴∠BEC=90°
∵∠A=∠BCE=60°.
∴∠EBC=30°,
∵OA=BC=2$\sqrt{3}$,
∴EC=$\sqrt{3}$,
∴OE=3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$,
∵四边形ECGB是菱形,∠BCE=60°,
∴△BEC是等边三角形,
∴BC=EC=2$\sqrt{3}$,
∴OE=3$\sqrt{3}$-2$\sqrt{3}$=$\sqrt{3}$;
(4)解:∵OE=x,
∴BG=CE=3$\sqrt{3}$-x,
∴S△BGC=$\frac{1}{2}$BG•OD=$\frac{1}{2}$×(3$\sqrt{3}$-x)×3=$\frac{9\sqrt{3}}{2}$-$\frac{3}{2}x$,
∴S四边形OAGC=S平行四边形OABC+S△BGC=3$\sqrt{3}$×3+$\frac{9\sqrt{3}}{2}$$-\frac{3}{2}$x=$\frac{27\sqrt{3}}{2}-\frac{3}{2}x$.
点评 本题主要考查了平行四边形的性质,含30°直角三角形的性质,矩形的性质,菱形的性质等,综合运用各性质定理,平行四边形和三角形的面积公式是解答此题的关键.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案x2-5x+(-$\frac{5}{2}$)2=(x-$\frac{5}{2}$)2;x2+3x+($\frac{3}{2}$)2=(x+$\frac{3}{2}$)2.
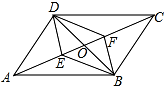 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| 比赛项目 | 比赛成绩/分 | ||
| 王晓丽 | 李真 | 林飞扬 | |
| 唱功 | 98 | 95 | 80 |
| 音乐常识 | 80 | 90 | 100 |
| 综合知识 | 80 | 90 | 100 |
(2)若按6:3:1的加权平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(3)若最后排名冠军是王晓丽,亚军是李真,季军是林飞扬,则权重可能是多少?
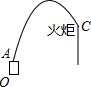 如图是某运动会开幕式点燃火炬的示意图,发射台OA的高度为2m,火炬的高度为12m,距发射台OA的水平距离为20m,在A处的发射装置向目标C发射一个火球点燃火炬,该火球运动的轨迹为抛物线形,当火球运动到距离地面最大高度20m时,相应的水平距离为12m,请你判断该火球能否点燃目标C?并说明理由.
如图是某运动会开幕式点燃火炬的示意图,发射台OA的高度为2m,火炬的高度为12m,距发射台OA的水平距离为20m,在A处的发射装置向目标C发射一个火球点燃火炬,该火球运动的轨迹为抛物线形,当火球运动到距离地面最大高度20m时,相应的水平距离为12m,请你判断该火球能否点燃目标C?并说明理由.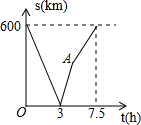 一列快车从起点甲地出发,匀速驶向终点乙地,与此同时,一列慢车从起点乙地出发,匀速驶向终点甲地,两车间的距离S(km)与慢车行驶的时间t(h)之间的函数关系图象如图所示,以下说法一定正确的个数有( )
一列快车从起点甲地出发,匀速驶向终点乙地,与此同时,一列慢车从起点乙地出发,匀速驶向终点甲地,两车间的距离S(km)与慢车行驶的时间t(h)之间的函数关系图象如图所示,以下说法一定正确的个数有( )