题目内容
2．如果某人沿坡度i=1：3的斜坡前进10m，那么他所在的位置比原来的位置升高了$\sqrt{10}$m．分析 根据题意作出图形，可得BC：AB=1：3，设BC=x，AB=3x，根据勾股定理可得AC2=AB2+BC2，代入求出x的值．
解答 解：
设BC=x，AB=3x，
则AC2=AB2+BC2，
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{10}$x=10，
解得：x=$\sqrt{10}$．
故所在的位置比原来的位置升高了$\sqrt{10}$m．
故答案为：$\sqrt{10}$．
点评 本题考查了坡度和坡角的知识，解答本题的关键是根据题意构造直角三角形，利用三角函数的知识求解．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
12．阅读下面材料：在数学课上，老师提出如下问题：
小涵的主要作法如下：
老师说：“小涵的做法正确的．”
请回答：小涵的作图依据是直径所对的圆周角是直角．
尺规作图，过圆外一点作圆的切线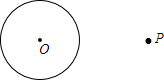． 已知：⊙O和点P 求过点P的⊙O的切线 |
| 如图，（1）连结OP，作线段OP的中点A； （2）以A为圆心，OA长为半径作圆，交⊙O于点B，C； （3）作直线PB和PC． 所以PB和PC就是所求的切线．  |
请回答：小涵的作图依据是直径所对的圆周角是直角．
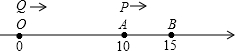如图，数轴上A，B两点对应的有理数分别为10和15，点P从点A出发，以每秒1个单位长度的速度沿数轴正方向运动，点Q同时从原点O出发，以每秒2个单位长度的速度沿数轴正方向运动，设运动时间为t秒．
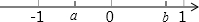已知：实数a，b在数轴上的位置如图所示，化简：$\sqrt{{{（a+1）}^2}}+2\sqrt{{{（b-1）}^2}}$-|a-b|．
17．将抛物线y=-（x+1）2向左平移1个单位后，得到的抛物线的顶点坐标是（ ）
| A． | （-2，0） | B． | （0，0） | C． | （-1，-1） | D． | （-2，-1） |
