题目内容
10.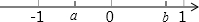 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{(a+1)}^2}}+2\sqrt{{{(b-1)}^2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{{{(a+1)}^2}}+2\sqrt{{{(b-1)}^2}}$-|a-b|.
分析 根据数轴上点的位置关系,可得a、b的大小,根据二次根式的性质,差的绝对值是大数减小数,可得答案.
解答 解:由数轴上点的位置关系,得
-1<a<0<b<1.
$\sqrt{{{(a+1)}^2}}+2\sqrt{{{(b-1)}^2}}$-|a-b|
=a+1+2(1-b)-(b-a)
=a+1+2-2b-b+a
=2a-3b+3.
点评 本题考查了实数与数轴,利用数轴上点的位置关系-1<a<0<b<1,又利用了二次根式的性质,差的绝对值是大数减小数.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
1.历史上,数学家欧拉最先把关于x的多项式用记号f(x)来表示,把x等于某数a时的多项式的值用f(a)来表示,例如x=-1时,多项式f(x)=x2+3x-5的值记为f(-1),那么f(-1)等于( )
| A. | -7 | B. | -9 | C. | -3 | D. | -1 |
18. 已知一次函数y=kx+b的图象如图所示,则下列判断中不正确的是( )
已知一次函数y=kx+b的图象如图所示,则下列判断中不正确的是( )
 已知一次函数y=kx+b的图象如图所示,则下列判断中不正确的是( )
已知一次函数y=kx+b的图象如图所示,则下列判断中不正确的是( )| A. | 方程kx+b=0的解是x=-3 | B. | k>0,b<0 | ||
| C. | 当x<-3时,y<0 | D. | y随x的增大而增大 |
15.德育处王主任将10份奖品分别放在10个完全相同的不透明礼盒中,准备将它们奖给小明等10位获“科技节活动先进个人”称号的同学.这些奖品中有5份是学习文具,3份是科普读物,2份是科技馆通票.小明同学从中随机取一份奖品,恰好取到科普读物的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
19.经专家测算,北京的4G网络速度基本上能够保证在80 000 000bps左右,最高峰值时曾达到106 000 000bps,将106 000 000用科学记数法表示应为( )
| A. | 106×106 | B. | 1.06×106 | C. | 1.06×108 | D. | 1.06×109 |
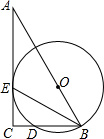 如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.