题目内容
12.如图,直线MN与x轴,y轴正半轴分别交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,直线y=x与直线MN交于点P,已知AC=10,OA=8.(1)求P点坐标;
(2)作∠AOP的平分线OQ交直线MN与点Q,点E、F分别为射线OQ、OA上的动点,连结AE与EF,试探索AE+EF是否存在最小值?若存在,请直接写出这个最小值;若不存在请说明理由;
(3)在直线MN上存在点G,使以点G,B,C三点为顶点的三角形是等腰三角形,请直接写出G点的坐标.

分析 (1)由AC与OA的长,利用勾股定理求出OC的长,确定出C坐标,利用待定系数法求出直线MN解析式,与y=x联立求出交点P坐标即可;
(2)作出相应的图形,如图1所示,作出A关于射线OQ的对称点A′,可得OA′=OA=8,过A′作A′F⊥OA,交射线OQ于点E,角射线OA于点F,此时A′E+EF=AE+EF存在最小值,求出即可;
(3)在直线MN上存在点G,使以点G,B,C三点为顶点的三角形是等腰三角形,分三种情况考虑:①PC=PB,此时P为线段BC垂直平分线与直线MN的交点;②PC=BC=8;③PB=BC=8,分别求出P坐标即可.
解答 解:(1)∵AC=10,OA=8,
∴OC=$\sqrt{A{C}^{2}-O{A}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴C(0,6);
设直线MN的解析式是y=kx+b(k≠0),
∵点A、C都在直线MN上,
∴$\left\{\begin{array}{l}{8k+b=0}\\{b=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=6}\end{array}\right.$,
∴直线MN的解析式为y=-$\frac{3}{4}$x+6,
∵P为y=-$\frac{3}{4}$x+6与直线y=x的交点.
∴-$\frac{3}{4}$x+6=x,
解得:x=$\frac{24}{7}$,
∴p的坐标为($\frac{24}{7}$,$\frac{24}{7}$);
(2)如图1所示: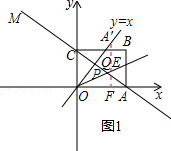
作出A关于射线OQ的对称点A′,可得OA′=OA=8,过A′作A′F⊥OA,交射线OQ于点E,角射线OA于点F,
此时A′E+EF=AE+EF存在最小值,在Rt△A′OF中,∠A′OF=45°,
设A′F=OF=x,根据勾股定理得:x2+x2=82,
解得:x=4$\sqrt{2}$,
则最小值为4$\sqrt{2}$;
(3)如图2所示: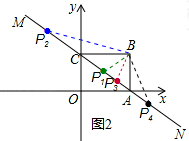
∵A(8,0),C(0,6),
∴根据题意得:B((8,6),
∵P在直线MN:y=-$\frac{3}{4}$x+6上,
∴设P(a,-$\frac{3}{4}$a+6),
在直线MN上存在点G,使以点G,B,C三点为顶点的三角形是等腰三角形,
分三种情况考虑:
①当PC=PB时,P点为BC垂直平分线与MN交点,此时P1(4,3);
②当PC=BC=8时,根据两点间的距离公式得:a2+(-$\frac{3}{4}$a+6-6)2=64,
解得:a=±$\frac{32}{5}$,
此时P2(-$\frac{32}{5}$,$\frac{54}{5}$),P3($\frac{32}{5}$,$\frac{6}{5}$);
③当PB=BC=8时,根据两点间的距离公式得:(a-8)2+(-$\frac{3}{4}$a+6-6)2=64,
解得:a=$\frac{256}{25}$,可得-$\frac{3}{4}$a+6=-$\frac{42}{25}$,此时P4($\frac{256}{25}$,-$\frac{42}{25}$),
则符合条件的点P有:P1(4,3),P2(-$\frac{32}{5}$,$\frac{54}{5}$),P3($\frac{32}{5}$,$\frac{6}{5}$),P4($\frac{256}{25}$,-$\frac{42}{25}$).
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,两点间的距离公式,待定系数法确定一次函数解析式,等腰三角形的性质,利用了分类讨论的思想,熟练掌握公式及法则是解本题的关键.

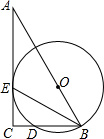 如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E. 如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.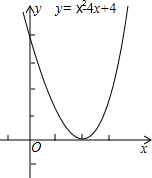 (1)抛物线与x轴有1个交点,它们的横坐标是2;
(1)抛物线与x轴有1个交点,它们的横坐标是2;