题目内容
20.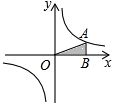 已知图中的曲线为函数y=$\frac{m}{x}$(m为常数,且m≠0)图象的一支.若A为该图象上一点,过点A作AB⊥x轴于点B,当△AOB的面积是2时,m的值为4.
已知图中的曲线为函数y=$\frac{m}{x}$(m为常数,且m≠0)图象的一支.若A为该图象上一点,过点A作AB⊥x轴于点B,当△AOB的面积是2时,m的值为4.
分析 求该反比例函数的函数表达式即求k值即可,S△AOB=$\frac{1}{2}$OB×AB=$\frac{1}{2}$xy=$\frac{1}{2}$m=2,由此求得m的值.
解答 解:设点A的坐标为(x,y),
由图可知x、y均为正数
即OB=x,AB=y.
∵△AOB的面积为2
∴S△AOB=$\frac{1}{2}$OB×AB=$\frac{1}{2}$xy=$\frac{1}{2}$m=2
可得m=4.
故答案是:4.
点评 主要考查了反比例函数$y=\frac{k}{x}$中k的几何意义,即图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.

练习册系列答案
相关题目
10.x是一个两位数,y是一个一位数,如果把y放在x的左边组成一个三位数,则此三位数可表示为( )
| A. | yx | B. | y+x | C. | 10y+x | D. | 100y+x |
11.如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”.若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等边三角形,则b的值为( )
| A. | ±2$\sqrt{3}$ | B. | ±$\frac{2\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
15.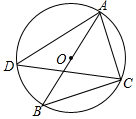 如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )
如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )
 如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )
如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
5.储蓄所先后办理了7笔业务,取出9.5万元,存入5万元,取出8万元,存入12万元,存入25万元,取出10.25万元,取出2万元,这时的存款比最初( )
| A. | 增加12.25万元 | B. | 减少12.25万元 | C. | 增加12万元 | D. | 减少12万元 |
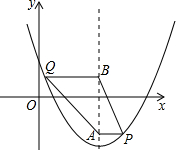 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(1,-1),且对称轴为直线x=2,点P、Q均在抛物线上,点P位于对称轴右侧,点Q位于对称轴左侧,PA垂直对称轴于点A,QB垂直对称轴于点B,且QB=PA+1,设点P的横坐标为m. 如图,在一块长为30米,宽为16米的长方形草地上,有两条宽都为1米的纵、横相交的小路,这块草地的绿地面积为435平方米.
如图,在一块长为30米,宽为16米的长方形草地上,有两条宽都为1米的纵、横相交的小路,这块草地的绿地面积为435平方米.