题目内容
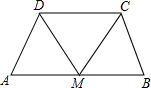 如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )
如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )| A、∠DAM=∠DCM |
| B、DM∥BC |
| C、△AMD≌△BMC |
| D、△AMD≌△DMC |
考点:等腰梯形的性质,全等三角形的判定
专题:
分析:根据等腰梯形同一底上的两个角相等可得∠A=∠B,再根据线段中点的定义可得AM=BM,然后利用“边角边”证明△AMD和△BMC全等,再根据平行四边形的判定与性质给出其它选项成立的条件.
解答:解:在等腰梯形ABCD中,∠A=∠B,
∵M是AB的中点,
∴AM=BM,
在△AMD和△BMC中,
,
∴△AMD≌△BMC(SAS),
只有当AB=2DC时,AM=BM=CD,
四边形AMCD和四边形BCDM是平行四边形,
∠DAM=∠DCM、DM∥BC、△AMD≌△DMC成立.
所以,说法正确的是C.
故选C.
∵M是AB的中点,
∴AM=BM,
在△AMD和△BMC中,
|
∴△AMD≌△BMC(SAS),
只有当AB=2DC时,AM=BM=CD,
四边形AMCD和四边形BCDM是平行四边形,
∠DAM=∠DCM、DM∥BC、△AMD≌△DMC成立.
所以,说法正确的是C.
故选C.
点评:本题考查了等腰梯形的性质,全等三角形的判定,熟记性质并确定出三角形全等的条件是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
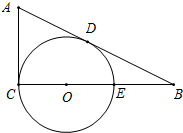 在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE.
在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE. 已知,如图△ABC中,I是内心,AI交BC于D,交△ABC的外接圆于点E,且∠B=60°,那么△IEC是等边三角形吗?说说你的理由.
已知,如图△ABC中,I是内心,AI交BC于D,交△ABC的外接圆于点E,且∠B=60°,那么△IEC是等边三角形吗?说说你的理由.