题目内容
10.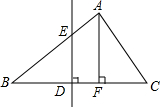 如图,在△ABC中,AB=4,AC=3,DE是BC的垂直平分线,交BC于点D,交AB于点E,AF⊥BC于点F.
如图,在△ABC中,AB=4,AC=3,DE是BC的垂直平分线,交BC于点D,交AB于点E,AF⊥BC于点F.(1)若∠BAC=90°,求AE的长;
(2)若DF=0.7,求证:△ABC为直角三角形.
分析 (1)连接CE,设AE=x,则BE=CE=x,利用勾股定理列出x的方程,求出x的值即可;
(2)设BD=y,则CD=y,用y表示出BF和CF,利用勾股定理列出y的方程,求出y的值,进而利用勾股定理的逆定理证明△ABC是直角三角形.
解答 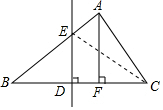 解:(1)连接CE,
解:(1)连接CE,
设AE=x,
∵AB=4,
∴BE=4-x,
∵DE是BC的垂直平分线,
∴CE=BE=4-x,
∵∠BAC=90°,AC=3,
∴x2+32=(4-x)2,
∴x=$\frac{7}{8}$,即AE=$\frac{7}{8}$.
(2)证明:设BD=y,则CD=y,
∵DF=0.7,
∴BF=y+0.7,CF=y-0.7,
∵AF⊥BC,
∴AB2-BF2=AC2-CF2=AF2,
∴42-(y+0.7)2=32-(y-0.7)2,
∴y=2.5,
∴BC=5,
∵32+42=52,
∴△ABC为直角三角形.
点评 本题主要考查了勾股定理以及勾股定理的逆定理的知识,解题的关键是掌握线段垂直平分线的性质,此题难度不大.

练习册系列答案
相关题目
18.已知2x=y,m是任意一个有理数,下列式子不一定成立的是( )
| A. | 2x-m=y-m | B. | 2mx=my | C. | 2x+$\frac{m}{4}$=y+$\frac{m}{4}$ | D. | $\frac{2x}{m-3}$=$\frac{y}{m-3}$ |
2.一个三角形的三边长分别为4,7,x,那么x可能的值是( )
| A. | 3 | B. | 7 | C. | 11 | D. | 15 |
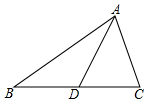 如图,△ABC中,AD是中线,AC=3,AB=5,则AD的取值范围是1<AD<4.
如图,△ABC中,AD是中线,AC=3,AB=5,则AD的取值范围是1<AD<4.