题目内容
我们把正六边形的顶点A、B、C、D、E、F及其对角线的交点O称作如图(1)所示的基本图的特征点,显然这样的基本图共有7个特征点.将此基本图不断复制并进行平行移动,使得相邻两个基本图的一边重合,这样得到图(2)、图(3),…
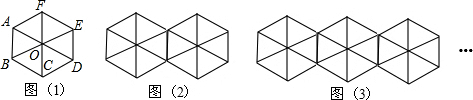
观察以上图形并完成下表:
(1)写出表中a的值是: ;
(2)猜想:在图(n)中,特征点的个数b的值是: (用含n的代数式表示).

观察以上图形并完成下表:
| 图形的名称 | 基本图的个数 | 特征点的个数 |
| 图(1) | 1 | 7 |
| 图(2) | 2 | 12 |
| 图(3) | 3 | 17 |
| 图(4) | 4 | a |
| … | … | … |
| 图(n) | n | b |
(2)猜想:在图(n)中,特征点的个数b的值是:
考点:规律型:图形的变化类
专题:
分析:观察图形,结合已知条件,得出将基本图每复制并平移一次,特征点增加5个,由此得出图4中特征点的个数为17+5=22个,进一步猜想出:在图(n)中,特征点的个数为:7+5(n-1)=5n+2;
解答:解:由题意,可知图1中特征点有7个;
图2中特征点有12个,12=7+5×1;
图3中特征点有17个,17=7+5×2;
所以图4中特征点有a=7+5×3=22个;
由以上猜想:在图(n)中,特征点的个数为:b=7+5(n-1)=5n+2;
故图中a=22,b=5n+2.
故答案为:22,5n+2.
图2中特征点有12个,12=7+5×1;
图3中特征点有17个,17=7+5×2;
所以图4中特征点有a=7+5×3=22个;
由以上猜想:在图(n)中,特征点的个数为:b=7+5(n-1)=5n+2;
故图中a=22,b=5n+2.
故答案为:22,5n+2.
点评:本题借助正六边形考查了规律型:图形的变化类问题,难度适中.关键是通过观察、归纳与总结,得到其中的规律

练习册系列答案
相关题目
若x2-x-n=(x-m)(x-3),则mn=( )
| A、6 | B、4 | C、12 | D、-12 |
 如图D、A、C、B为⊙O上的点,DC=AB,则AD与BC的大小关系是( )
如图D、A、C、B为⊙O上的点,DC=AB,则AD与BC的大小关系是( )| A、AD>BC | B、AD=BC |
| C、AD<BC | D、不能确定 |
 如图,?ABCD的两条对角线线交于O,且
如图,?ABCD的两条对角线线交于O,且