题目内容
认真阅读材料,然后回答问题:
我们初中学习了多项式的运算法则,相应的我们可以计算出多项式的展开式,如:(a+b)1=a+b,
(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…
下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数是可以单独列成表中的形式:

上面的多项式展开系数表称为“杨辉三角形”;仔细观察“杨辉三角形”,用你发现的规律回答下列问题:
(1)(a+b)n展开式中共有多少项?
(1)请写出多项式(a+b)5的展开式?
(2)请根据上面的规律计算25-5×24+10×23-10×22+5×2-15.
我们初中学习了多项式的运算法则,相应的我们可以计算出多项式的展开式,如:(a+b)1=a+b,
(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…
下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数是可以单独列成表中的形式:

上面的多项式展开系数表称为“杨辉三角形”;仔细观察“杨辉三角形”,用你发现的规律回答下列问题:
(1)(a+b)n展开式中共有多少项?
(1)请写出多项式(a+b)5的展开式?
(2)请根据上面的规律计算25-5×24+10×23-10×22+5×2-15.
考点:整式的混合运算
专题:规律型
分析:(1)由题意可求得当n=1,2,3,4,…时,多项式(a+b)n的展开式是一个几次几项式,然后找规律,即可求得答案;
(2)通过观察可以看出(a+b)5的展开式为5次6项式,a的次数按降幂排列,b的次数按升幂排列,各项系数分别为1,5,10,10,5,1;
(3)根据题意得出原式=(2-1)5,进而得出答案.
(2)通过观察可以看出(a+b)5的展开式为5次6项式,a的次数按降幂排列,b的次数按升幂排列,各项系数分别为1,5,10,10,5,1;
(3)根据题意得出原式=(2-1)5,进而得出答案.
解答:解:(1)∵当n=1时,多项式(a+b)1的展开式是一次二项式,
当n=2时,多项式(a+b)2的展开式是二次三项式,
当n=3时,多项式(a+b)3的展开式是三次四项式,
当n=4时,多项式(a+b)4的展开式是四次五项式,
…
∴多项式(a+b)n的展开式是一个n次n+1项式;
即(a+b)n展开式中共有n+1项;
(2)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
(3)由题意可得:25-5×24+10×23-10×22+5×2-15=(2-1)5=1.
当n=2时,多项式(a+b)2的展开式是二次三项式,
当n=3时,多项式(a+b)3的展开式是三次四项式,
当n=4时,多项式(a+b)4的展开式是四次五项式,
…
∴多项式(a+b)n的展开式是一个n次n+1项式;
即(a+b)n展开式中共有n+1项;
(2)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
(3)由题意可得:25-5×24+10×23-10×22+5×2-15=(2-1)5=1.
点评:此题考查数字的规律,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
下列命题为真命题的是( )
| A、若直线y=-kx+2过二、四象限,则k>0 |
| B、有两边和一角分别相等的两个三角形全等 |
| C、直线y=2x-3在y轴上的截距为3 |
| D、△ABC中,若∠A=2∠B=3∠C,那么△ABC为直角三角形 |
 如图,A、B是函数y=
如图,A、B是函数y=| 2 |
| x |
| A、S=2 | B、S=4 |
| C、S=8 | D、S=1 |
下列四张印有汽车品牌标志图案的卡片中,是中心对称图形的卡片是( )
A、 |
B、 |
C、 |
D、 |
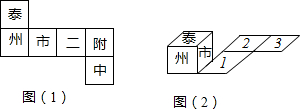 如图(1),是一个正方体的侧面展开图,小正方体从图(2)的位置依次翻到第1格、第2格、第3格,当小正方体在第3格时,朝上面的字是( )
如图(1),是一个正方体的侧面展开图,小正方体从图(2)的位置依次翻到第1格、第2格、第3格,当小正方体在第3格时,朝上面的字是( )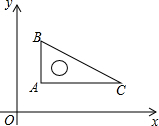 如图,在平面直角坐标系中,直角三角板∠C=30°,AB=4,将直角顶点放在点(
如图,在平面直角坐标系中,直角三角板∠C=30°,AB=4,将直角顶点放在点( 如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2的解集为
如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2的解集为