题目内容
直角三角形ABC中，∠C=90°，∠A=30°，BD平分∠ABC交AC于D，如果D到AB的距离为2，则AC-BD= ．
考点：角平分线的性质
专题：
分析：过D作DE⊥AB于点E，则可求得AD=BD=4，则AC-BD=AC-AD=CD，可求得答案．
解答：
解：如图，过D作DE⊥AB于点E，
∵∠C=90°，∠A=30°，
∴∠ABC=60°，
∵BD平分∠ABC，
∴∠DBA=∠A=30°，DE=CD=2，
∴BD=AD，
∴AC-BD=AC-AD=CD=2，
故答案为：2．
解：如图，过D作DE⊥AB于点E，∵∠C=90°，∠A=30°，
∴∠ABC=60°，
∵BD平分∠ABC，
∴∠DBA=∠A=30°，DE=CD=2，
∴BD=AD，
∴AC-BD=AC-AD=CD=2，
故答案为：2．
点评：本题主要考查角平分线的性质和等腰三角形的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．
练习册系列答案
相关题目
下列变形正确的是（ ）
| A、由5=x-2得x=-5-2 | ||
B、由5y=0得y=
| ||
| C、由2x=3x+5得-5=3x-2x | ||
D、由3x=-2得x=-
|
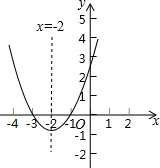已知二次函数y=x2+4x+3，回答下列问题：