题目内容
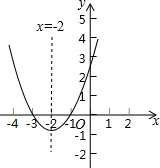 已知二次函数y=x2+4x+3,回答下列问题:
已知二次函数y=x2+4x+3,回答下列问题:(1)说出此抛物线的对称轴和顶点坐标;
(2)写出抛物线与x轴交点A、B的坐标,与y轴的交点C的坐标;
(3)写出函数的最值和增减性;
(4)x取何值时,①y<0,②y>0.
考点:二次函数的性质,二次函数的图象
专题:计算题
分析:(1)把抛物线解析式配成顶点式,即可得到抛物线的对称轴和顶点坐标;
(2)求自变量为0时的函数值即可得到C点坐标;求函数值为0时的自变量的值即可得到点A和点B的坐标;
(3)根据二次函数的性质求解;
(4)①根据函数图象,找出函数图象在x轴下方所对应的自变量的取值范围;
②根据函数图象,找出函数图象在x轴上方所对应的自变量的取值范围.
(2)求自变量为0时的函数值即可得到C点坐标;求函数值为0时的自变量的值即可得到点A和点B的坐标;
(3)根据二次函数的性质求解;
(4)①根据函数图象,找出函数图象在x轴下方所对应的自变量的取值范围;
②根据函数图象,找出函数图象在x轴上方所对应的自变量的取值范围.
解答:解:(1)y=x2+4x+3=(x+2)2-1,
故抛物线的对称轴为直线x=-2,顶点坐标为(-2,-1);
(2)当x=0时,y=x2+4x+3=3,
则C点坐标为(0,2);
当y=0时,x2+4x+3=0,解得x1=-3,x2=-1.
则A点坐标为(-3,0),B点坐标为(-1,0);
(3)二次函数有最小值-1;当x<-2时,y随x的增大而减小,当x>-2时,y随x的增大而增大;
(4)①当-3<x<-1时,y<0;
②当x<-3或x>-1时,y>0.
故抛物线的对称轴为直线x=-2,顶点坐标为(-2,-1);
(2)当x=0时,y=x2+4x+3=3,
则C点坐标为(0,2);
当y=0时,x2+4x+3=0,解得x1=-3,x2=-1.
则A点坐标为(-3,0),B点坐标为(-1,0);
(3)二次函数有最小值-1;当x<-2时,y随x的增大而减小,当x>-2时,y随x的增大而增大;
(4)①当-3<x<-1时,y<0;
②当x<-3或x>-1时,y>0.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=2x+b的图象与两坐标轴围成的三角形的面积为4,则函数的表达式为( )
| A、y=2x+4 |
| B、y=2x-4 |
| C、y=2x+4或 y=2x-4 |
| D、y=-2x-4 |
在实数-
,0.
,
,
,0.1010010001,
中,无理数的个数为( )
| 5 |
| • |
| 2 |
| • |
| 1 |
| π |
| 3 |
| 22 |
| 7 |
| 3 | 8 |
| A、1个 | B、2个 | C、3个 | D、4个 |
今年十一黄金周,蚌埠市各旅游景区、农家乐共接待游客182万人次,182万用科学记数法表示为( )
| A、1.82×105 |
| B、18.2×105 |
| C、1.82×106 |
| D、0.182×107 |
 如图,BD为△ABC的角平分线,CF为△ABC的外角∠ACE的平分线,它与BD的延长线交于点F.求证:∠A=2∠F.
如图,BD为△ABC的角平分线,CF为△ABC的外角∠ACE的平分线,它与BD的延长线交于点F.求证:∠A=2∠F.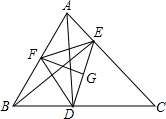 在△ABC中,AD⊥BC于点D,BE⊥AC于点E,F是AB的中点,FG⊥DE于点G,求证:∠DFG=∠EFG.
在△ABC中,AD⊥BC于点D,BE⊥AC于点E,F是AB的中点,FG⊥DE于点G,求证:∠DFG=∠EFG.