题目内容
已知M是满足不等式-
<a<
的所有整数a的和,N是满足不等式x≤
的最大整数.求M+N的平方根.
| 3 | 6 |
| 3 | 24 |
| ||
| 2 |
考点:估算无理数的大小
专题:
分析:首先估计出:-
<-
<-
,2<
<
,进而得出M的值,再估计出N的值进而得出答案.
| 3 | 8 |
| 3 | 6 |
| 3 | 1 |
| 3 | 24 |
| 3 | 27 |
解答:解:∵-
<-
<-
,2<
<
,
∴不等式-
<a<
的所有整数为:-1,0,1,2,
∴M=2,
∵10<
<11,
∴N是满足不等式x≤
的最大整数为:4,
∴M+N=6,
故M+N的平方根为:±
.
| 3 | 8 |
| 3 | 6 |
| 3 | 1 |
| 3 | 24 |
| 3 | 27 |
∴不等式-
| 3 | 6 |
| 3 | 24 |
∴M=2,
∵10<
| 110 |
∴N是满足不等式x≤
| ||
| 2 |
∴M+N=6,
故M+N的平方根为:±
| 6 |
点评:此题主要考查了估算无理数的大小,正确估计出无理数接近的有理数是解题关键.

练习册系列答案
相关题目
下列方程中,一元一次方程是( )
| A、2y=1 |
| B、3x-5 |
| C、3+7=10 |
| D、x2+x=1 |
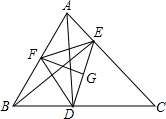 在△ABC中,AD⊥BC于点D,BE⊥AC于点E,F是AB的中点,FG⊥DE于点G,求证:∠DFG=∠EFG.
在△ABC中,AD⊥BC于点D,BE⊥AC于点E,F是AB的中点,FG⊥DE于点G,求证:∠DFG=∠EFG. 如图,∠AOB和∠COD具有公共顶点O,且∠AOB=∠COD=90°.若∠AOD是∠BOC的5倍,则∠BOC=
如图,∠AOB和∠COD具有公共顶点O,且∠AOB=∠COD=90°.若∠AOD是∠BOC的5倍,则∠BOC=