题目内容
在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=3cm,BD=4cm,则此梯形的面积为 cm2,梯形的高为 cm.
考点:梯形
专题:
分析:过D作DE∥AC交BC的延长线于E,AC交BD于O,过D作DH⊥BC于H,得到平行四边形,推出AC=DE=3cm,由AC⊥BD,推出∠BDE=∠BOC=90°,根据勾股定理求出BE,根据三角形的面积公式得到BD×DE=BE×DH,求出DH,根据梯形的面积是
(AD+BC)•DH代入计算即可.
| 1 |
| 2 |
解答:解:过D作DE∥AC交BC的延长线于E,AC交BD于O,过D作DH⊥BC于H,
∵AD∥BC,DE∥AC,
∴四边形ADEC是平行四边形,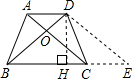
∴AC=DE=3cm,AD=CE,
∵AC⊥BD,
∴∠BDE=∠BOC=90°,
由勾股定理得:BE=
=5,
即AD+BC=BE=5
根据三角形的面积公式得:BD×DE=BE×DH,
×3×4=
×5DH,
∴DH=2.4cm,
∴梯形的面积是
(AD+BC)•DH=6cm2.
故答案为:6,2.4.
∵AD∥BC,DE∥AC,
∴四边形ADEC是平行四边形,

∴AC=DE=3cm,AD=CE,
∵AC⊥BD,
∴∠BDE=∠BOC=90°,
由勾股定理得:BE=
| BD2+DE2 |
即AD+BC=BE=5
根据三角形的面积公式得:BD×DE=BE×DH,
| 1 |
| 2 |
| 1 |
| 2 |
∴DH=2.4cm,
∴梯形的面积是
| 1 |
| 2 |
故答案为:6,2.4.
点评:本题主要考查对梯形的性质,平行线的性质和判定,平行四边形的性质和判定,三角形的面积,勾股定理等知识点的理解和掌握,根据性质求出高DH和AD+BC的长是解此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
若⊙O1、⊙O2的半径分别为4和6,圆心距O1O2=2,则⊙O1与⊙O2的位置关系是( )
| A、相交 | B、内切 | C、外切 | D、外离 |
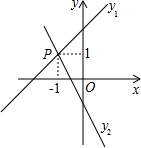 如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),关于x的不等式x+m>kx-1的解集是( )
如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),关于x的不等式x+m>kx-1的解集是( )| A、x≥-1 | B、x>-1 |
| C、x≤-1 | D、x<-1 |
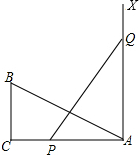 如图,BC、AX分别垂直于AC,AC=2BC,点P和点Q从A点出发分别在AC和射线AX上运动,且点Q的运动速度是点P运动速度的2倍,当点P运动到
如图,BC、AX分别垂直于AC,AC=2BC,点P和点Q从A点出发分别在AC和射线AX上运动,且点Q的运动速度是点P运动速度的2倍,当点P运动到