题目内容
14. 2015年12月19日郑州机场T2航站楼正式启用,为了宣传T2航站楼,机场反面要印刷一批宣传材料,经招标,某印务公司中标,该印务公司提出3种方案:
2015年12月19日郑州机场T2航站楼正式启用,为了宣传T2航站楼,机场反面要印刷一批宣传材料,经招标,某印务公司中标,该印务公司提出3种方案:方案一:每份材料收印刷费1元;
方案二:收制版费1000元,另外每份材料收印刷费m元;
方案三:印数在1000份以内时,每份材料收印刷费1.2元,超过1000份时超过部分按每份n元收取.
(1)若机场方面选用方案二和方案三各印刷2000份材料需花费3900元,选用方案二和方案三各印刷3000份材料需花费5100元,请求出m和n的值;
(2)分别写出各方案的收费y(元)与印刷材料的份数x(份)之间的函数关系式;
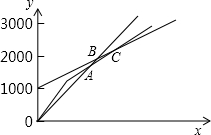
(3)若机场方面预计要印刷5000份以内的宣传材料,请根据图象求出A、B、C的坐标,并直接写出机场方面应选择哪一种方案更合算?
分析 (1)根据:“选用方案二和方案三各印刷2000份材料需花费3900元,选用方案二和方案三各印刷3000份材料需花费5100元”列出关于m、n的方程组求解即可;
(2)根据三种方案不同收费方式分别列出函数解析式即可;
(3)利用函数交点坐标求法分别得出即可;利用A、B、C的点的坐标以及结合得出函数图象得出答案.
解答 解:(1)根据题意,得:$\left\{\begin{array}{l}{1000+2000m+1200+1000n=3900}\\{1000+3000m+1200+2000n=5100}\end{array}\right.$,
整理,得:$\left\{\begin{array}{l}{20m+10n=17}\\{30m+20n=29}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=0.5}\\{n=0.7}\end{array}\right.$;
(2)方案一:y=x;
方案二:y=1000+0.5x;
方案三:①当0≤x≤1000时,y=1.2x,
②当x>1000时,y=1200+0.7(x-1000)=0.7x+500,
综上:y=$\left\{\begin{array}{l}{1.2x}&{(0≤x≤1000)}\\{0.7x+500}&{(x>1000)}\end{array}\right.$;
(3)联立方程组$\left\{\begin{array}{l}{y=x}\\{y=0.7x+500}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=1666\frac{2}{3}}\\{y=1666\frac{2}{3}}\end{array}\right.$,
故点A的坐标为(1666$\frac{2}{3}$,1666$\frac{2}{3}$);
联立方程组$\left\{\begin{array}{l}{y=x}\\{y=0.5x+1000}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2000}\\{y=2000}\end{array}\right.$,
故点B的坐标为(2000,2000);
联立方程组$\left\{\begin{array}{l}{y=0.5x+1000}\\{y=0.7x+500}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2500}\\{y=2250}\end{array}\right.$,
故点C坐标为(2500,2250);
由图象可知,当0≤x≤1666$\frac{2}{3}$时,选择方案一费用最低;
当1666$\frac{2}{3}$<x<2500时,选择方案三费用最低;
当x=2500时,选择方案二、方案三费用一样;
当x>2500时,选择方案二费用最低.
点评 此题主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,数形结合得出自变量的取值范围得出是解题关键.

| A. | x2+y=0 | B. | $\frac{x+y}{3}$-2y=1 | C. | x=$\frac{2}{y}$+1 | D. | y+$\frac{1}{2}$x |
| A. | 2x+1≤-3 | B. | 2x-1≥-3 | C. | -2x+1≥3 | D. | -2x-1≤3 |
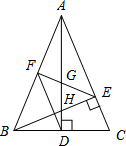 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )