题目内容
17.下列化简或计算正确的是( )| A. | $\sqrt{(-\sqrt{3})^{2}}$=-$\sqrt{3}$ | B. | $\sqrt{1\frac{1}{49}}$=1+$\frac{1}{7}$=$\frac{8}{7}$ | C. | ($\sqrt{6}-\sqrt{3}$)2=9-2$\sqrt{3}$ | D. | $\sqrt{24}$÷(-$\frac{1}{2}$$\sqrt{6}$)=-4 |
分析 根据二次根式的性质对A、B进行判断;根据完全平方公式对C进行判断;根据二次根式的除法法则对D进行判断.
解答 解:A、原式=|-$\sqrt{3}$|=$\sqrt{3}$,所以A选项错误;
B、原式=$\sqrt{\frac{50}{49}}$=$\frac{5\sqrt{2}}{7}$,所以B选项错误;
C、原式=6-6$\sqrt{2}$+3=9-6$\sqrt{2}$,所以C选项错误;
D、原式=-2$\sqrt{24÷6}$=-4,所以D选项正确.
故选D.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.解方程组$\left\{\begin{array}{l}{26x+29y=3,(1)}\\{29x+26y=-3,(2)}\end{array}\right.$,下列四种方法中,最简便的是( )
| A. | 代入消元法 | B. | (1)×29-(2)×26,先消去x | ||
| C. | (1)×26-(2)×29,先消去y | D. | (1)+(2),两方程相加 |
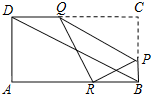 如图,在矩形ABCD中,AB=3,AD=$\sqrt{3}$,点P在边BC上的,过点P作PQ∥BD,交CD边于Q点,再把△PQC沿PQ对折,点C的对应点R恰好落在AB边上,则CP=$\frac{2\sqrt{3}}{3}$.
如图,在矩形ABCD中,AB=3,AD=$\sqrt{3}$,点P在边BC上的,过点P作PQ∥BD,交CD边于Q点,再把△PQC沿PQ对折,点C的对应点R恰好落在AB边上,则CP=$\frac{2\sqrt{3}}{3}$.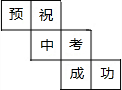 一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )
一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )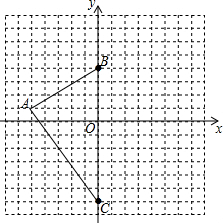 已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).
已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).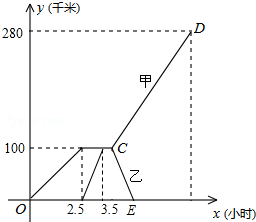 已知,A、B两市相距280千米,甲车从A市前往B市运送物资,行驶2.5小时在M地汽车M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计).乙车到达M地后又经过30分钟修好甲车后原路返回,同时甲车以原速1.5倍的速度前往B市.如图是甲、乙两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
已知,A、B两市相距280千米,甲车从A市前往B市运送物资,行驶2.5小时在M地汽车M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计).乙车到达M地后又经过30分钟修好甲车后原路返回,同时甲车以原速1.5倍的速度前往B市.如图是甲、乙两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题: