题目内容
2.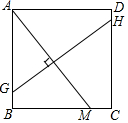 如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.
如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.
分析 作平行线,构建全等三角形,证明△ABM≌△BCE,得AM=BE,再证明四边形GBEH是平行四边形得GH=BE,所以GH=AM,由勾股定理计算出AM的长即可.
解答 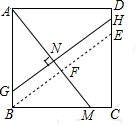 解:过B作BE∥GH,交DC于E,
解:过B作BE∥GH,交DC于E,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCE=90°,
∴∠EBC+∠BEC=90°,
∵GH是AM的中垂线,BE∥GH,
∴∠BFM=∠GNM=90°,
∴∠EBC+∠BMF=90°,
∴∠BEC=∠BMF,
∴△ABM≌△BCE,
∴AM=BE,
∵AB=BC=8,MC=2,
∴BM=BC-MC=8-2=6,
∴AM=10,
∴BE=10,
∵BG∥EH,GH∥BE,
∴四边形GBEH是平行四边形,
∴GH=BE=10.
点评 本题考查了正方形、线段垂直平分线的性质,把所求的边利用三角形全等和平行四边形转化到直角△ABM中,使问题得以解决,直角三角形中的边利用勾股定理求出,做好此题要熟练掌握正方形的各边相等及各角为90°,在正方形中证明三角形全等,常根据同角的余角相等来证明角的大小关系.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
14. 如图(1),将一个边长为2的正方形分割成四个完全相同的直角三角形,然后把这4个直角三角形无缝隙不重叠的拼成如图(2)所示的大正方形,若图(2)中的小正方形边长是1,则图(2)中大正方形的边长是( )
如图(1),将一个边长为2的正方形分割成四个完全相同的直角三角形,然后把这4个直角三角形无缝隙不重叠的拼成如图(2)所示的大正方形,若图(2)中的小正方形边长是1,则图(2)中大正方形的边长是( )
 如图(1),将一个边长为2的正方形分割成四个完全相同的直角三角形,然后把这4个直角三角形无缝隙不重叠的拼成如图(2)所示的大正方形,若图(2)中的小正方形边长是1,则图(2)中大正方形的边长是( )
如图(1),将一个边长为2的正方形分割成四个完全相同的直角三角形,然后把这4个直角三角形无缝隙不重叠的拼成如图(2)所示的大正方形,若图(2)中的小正方形边长是1,则图(2)中大正方形的边长是( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
11.在平面直角坐标中,将直线l1:y=2x平移后,得到直线l1:y=2x+6,则下列平移说法正确的是( )
| A. | 将l1向上平移6个单位长度 | B. | 将l1向下平移6个单位长度 | ||
| C. | 将l1向左平移6个单位长度 | D. | 将l1向右平移6个单位长度 |
8. 如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
 如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )| A. | $\overrightarrow{AD}$=$\overrightarrow{EB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{DC}$ | C. | $\overrightarrow{AB}$=$\overrightarrow{DE}$ | D. | $\overrightarrow{AD}$=$\overrightarrow{EC}$ |
 如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.
如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.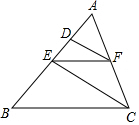 如图EF∥BC,DF∥CE,求证:AE2=AD•AB.
如图EF∥BC,DF∥CE,求证:AE2=AD•AB.