如图(1).将一个边长为2的正方形分割成四个完全相同的直角三角形.然后把这4个直角三角形无缝隙不重叠的拼成如图(2)所示的大正方形.若图(2)中的小正方形边长是1.则图(2)中大正方形的边长是( )A．2B．$\sqrt{5}$C．$\sqrt{6}$D．$\sqrt{7}$ 题目和参考答案——青夏教育精英家教网—

题目内容

14．

如图（1），将一个边长为2的正方形分割成四个完全相同的直角三角形，然后把这4个直角三角形无缝隙不重叠的拼成如图（2）所示的大正方形，若图（2）中的小正方形边长是1，则图（2）中大正方形的边长是（　　）

A．

B．

$\sqrt{5}$

C．

$\sqrt{6}$

D．

$\sqrt{7}$

分析直接利用勾股定理得出正方形的边长，进而得出答案．

解答解：由题意可得：BC=1，DC=1，AC=2，
故AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
则图（2）中大正方形的边长是：$\sqrt{5}$．

点评此题主要考查了图形的剪拼以及勾股定理，正确应用勾股定理是解题关键．

练习册系列答案

相关题目

4．下列二次根式中与$\sqrt{2}$能合并的是（　　）

2．

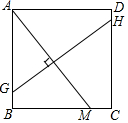如图所示，在正方形ABCD中，M是BC上一点，连接AM，作AM垂直平分线GH交AB于G点，交CD于H点，已知AB=8，CM=2，求GH长．

9．

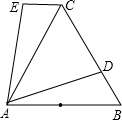如图，△ABC为等边三角形，D是BC边上一点，AB=10，AD=9，△ABD经过旋转60°后到达△ACE的位置，
（1）求∠DAE的度数．
（2）△DCE的周长是多少？

19．

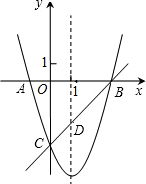如图，已知抛物线y=x²+bx+c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，-3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．
（1）求抛物线的函数表达式；
（2）点M是抛物线上一点，当△ABM的面积等于△ABC的面积时，求点M的坐标
（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．
①当线段PQ=$\frac{3}{4}$AB时，求∠CED的余切值；
②点G是直线x=1上一点，当△CEG与△AOC相似时，请直接写出点E的坐标．

6．已知y=$\sqrt{x-3}$+$\sqrt{3-x}$+5，则x²-xy+y²=19．

3．设p是大于2的质数，求方程$\frac{2}{p}$=$\frac{1}{x}$+$\frac{1}{y}$的正整数解．

20．若互不相等的实数a，b，c满足a+$\frac{2}{b+c}$=c+$\frac{2}{c+a}$，及b+$\frac{2}{c+a}$=a+$\frac{2}{a+b}$，则（a+b）（b+c）（c+a）等于（　　）

试题分类