题目内容
7．在平面直角坐标系中，把一条抛物线先向上平移3个单位长度，然后绕原点旋转180°得到抛物线y=x2+5x+6，则原抛物线的解析式是y=-（x-$\frac{5}{2}$）2-$\frac{11}{4}$．分析 先求出绕原点旋转180°的抛物线解析式，求出向下平移3个单位长度的解析式即可．
解答 解：∵抛物线的解析式为：y=x2+5x+6，
设原抛物线上有点（x，y），绕原点旋转180°后，变为（-x，-y），点（-x，-y）在抛物线y=x2+5x+6上，
将（-x，-y）代入y=x2+5x+6得-y=x2-5x+6，所以原抛物线的方程为y=-x2+5x-6=-（x-$\frac{5}{2}$）2+$\frac{1}{4}$，
∴向下平移3个单位长度的解析式为y=-（x-$\frac{5}{2}$）2+$\frac{1}{4}$-3=-（x-$\frac{5}{2}$）2-$\frac{11}{4}$，
故答案为：y=-（x-$\frac{5}{2}$）2-$\frac{11}{4}$．
点评 本题考查的是二次函数的图象与几何变换，熟知二次函数的图象旋转及平移的法则是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．下列各式中，不是同类项的是（ ）
| A． | $\frac{1}{2}$ab和5ba | B． | a3和53 | C． | $\frac{xy}{5}$和52xy | D． | 102和$\frac{1}{10}$ |
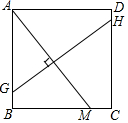如图所示，在正方形ABCD中，M是BC上一点，连接AM，作AM垂直平分线GH交AB于G点，交CD于H点，已知AB=8，CM=2，求GH长．
如图，小张和小刘身高相同，在灯光下，小张的影子比小刘的影子长，这说明小张比小刘距离灯光远．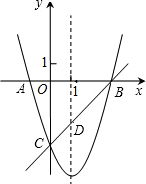
如图，已知抛物线y=x2+bx+c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，-3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．
16．等边三角形的内切圆半径为r，外接圆半径为R，高为h，则r：R：h的值为（ ）
| A． | 1：2：3 | B． | 1：$\sqrt{3}$：2 | C． | 1：$\sqrt{2}$：2 | D． | 1：$\sqrt{2}$：$\sqrt{3}$ |
