题目内容
13.(1)2sin260°-$\sqrt{3}$tan30°-2cos245°+$\frac{1}{2tan45°}$;(2)$\frac{2sin30°}{4cos60°-1}$+$\frac{cos30°}{tan60°}$.
分析 (1)、(2)直接把各特殊角的三角函数值代入进行计算即可.
解答 解:(1)原式=2×($\frac{\sqrt{3}}{2}$)2-$\sqrt{3}$×$\frac{\sqrt{3}}{3}$-2×($\frac{\sqrt{2}}{2}$)2+$\frac{1}{2}$
=2×$\frac{3}{4}$-1-2×$\frac{1}{2}$+$\frac{1}{2}$
=$\frac{3}{2}$-1-1+$\frac{1}{2}$
=0;
(2)原式=$\frac{2×\frac{1}{2}}{4×\frac{1}{2}-1}$+$\frac{\frac{\sqrt{3}}{2}}{\sqrt{3}}$
=$\frac{1}{2-1}$+$\frac{1}{2}$
=1+$\frac{1}{2}$
=$\frac{3}{2}$.
点评 本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
3.如果将抛物线y=x2+2向左平移1个单位,那么所得新抛物线的解析式为( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=x2+1 | D. | y=x2+3 |
4.下列二次根式中与$\sqrt{2}$能合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{18}$ |
1.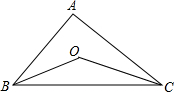 如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
 如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )| A. | 95° | B. | 120° | C. | 135° | D. | 无法确定 |
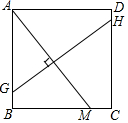 如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.
如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.