题目内容
10. 如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.
如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.
分析 先根据等边△OAD和等边△ABC的性质,得出∠OAD=∠BAC=60°,OA=DA,BA=CA,进而判定△OAB≌△DAC,最后根据全等三角形的性质,得出OB=DC.
解答 证明:∵等边△OAD和等边△ABC,
∴∠OAD=∠BAC=60°,OA=DA,BA=CA,
∴∠OAB=∠DAC,
在△OAB和△DAC中,
$\left\{\begin{array}{l}{OA=DA}\\{∠OAB=∠DAC}\\{BA=CA}\end{array}\right.$,
∴△OAB≌△DAC(SAS),
∴OB=DC.
点评 本题主要考查了全等三角形的判定与性质以及等边三角形的性质的运用,解题时注意:等边三角形的三个内角都相等,且都等于60°.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.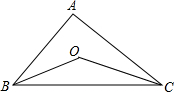 如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
 如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )
如图,点O是△ABC内一点,∠A=90°,∠ABC与∠ACB的角平分线BO,CO相交点O,则∠BOC等于( )| A. | 95° | B. | 120° | C. | 135° | D. | 无法确定 |
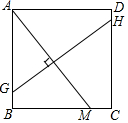 如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.
如图所示,在正方形ABCD中,M是BC上一点,连接AM,作AM垂直平分线GH交AB于G点,交CD于H点,已知AB=8,CM=2,求GH长.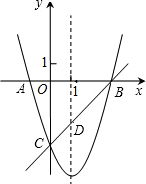 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.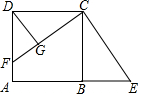 如图,正方形ABCD中,AB=20,F为AD上的点,连接CF,作CE⊥CF交AB的延长线于点E,作DG⊥CF于点G,若BE=15,CE=25,则DG的长度为12.
如图,正方形ABCD中,AB=20,F为AD上的点,连接CF,作CE⊥CF交AB的延长线于点E,作DG⊥CF于点G,若BE=15,CE=25,则DG的长度为12.