题目内容
17．
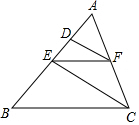如图EF∥BC，DF∥CE，求证：AE2=AD•AB．
分析 由EF∥BC，DF∥CE，可证得△AEF∽△ABC，△ADF∽△AEC，然后由相似三角形的对应边成比例，证得结论．
解答 证明：∵EF∥BC，DF∥CE，
∴△AEF∽△ABC，△ADF∽△AEC，
∴AE：AB=AF：AC，AD：AE=AF：AC，
∴AE：AB=AD：AE，
∴AE2=AD•AB．
点评 此题考查了相似三角形的判定与性质．注意证得△AEF∽△ABC，△ADF∽△AEC是关键．
练习册系列答案
相关题目
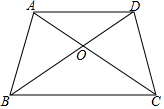已知梯形ABCD如图，AD∥BC，△AOD的面积是25，△DOC的面积是35，则梯形ABCD的面积是144．
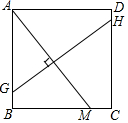如图所示，在正方形ABCD中，M是BC上一点，连接AM，作AM垂直平分线GH交AB于G点，交CD于H点，已知AB=8，CM=2，求GH长．
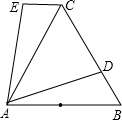如图，△ABC为等边三角形，D是BC边上一点，AB=10，AD=9，△ABD经过旋转60°后到达△ACE的位置，