题目内容
11.先化简,后求值:$\frac{2x}{{{x^2}-4}}$-$\frac{1}{x-2}$,其中x=$\sqrt{2}$-2.分析 根据分式的减法和约分的方法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:$\frac{2x}{{{x^2}-4}}$-$\frac{1}{x-2}$
=$\frac{2x-(x+2)}{(x+2)(x-2)}$
=$\frac{2x-x-2}{(x+2)(x-2)}$
=$\frac{x-2}{(x+2)(x-2)}$
=$\frac{1}{x+2}$,
当x=$\sqrt{2}$-2时,原式=$\frac{1}{\sqrt{2}-2+2}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.下列各组值代表线段的长度(单位为:cm),则不能够构成三角形的是( )
| A. | 5,6,7 | B. | 2,3,4 | C. | 3,6,9 | D. | 5,12,13 |
2.化简-5ab+4ab的结果是( )
| A. | -1 | B. | a | C. | -ab | D. | b |
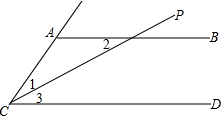 已知AB∥CD,CP平分∠ACD.求证:∠1=∠2
已知AB∥CD,CP平分∠ACD.求证:∠1=∠2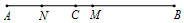 如图,线段AB=8cm,C是线段AB上一点,AC=3.2cm,M是AB的中点,N是AC的中点.
如图,线段AB=8cm,C是线段AB上一点,AC=3.2cm,M是AB的中点,N是AC的中点.