题目内容
19．
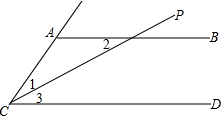已知AB∥CD，CP平分∠ACD．求证：∠1=∠2证明：∵AB∥CD（已知），
∴∠2=∠3 （两直线平行，内错角相等）．
又∵CP平分∠ACD，∴∠1=∠3．
∴∠1=∠2（等量代换）．
分析 先根据平行线的性质，得出∠2=∠3，再根据角平分线的定义以及等量代换，即可得到结论．
解答 证明：∵AB∥CD（已知），
∴∠2=∠3 （两直线平行，内错角相等）．
又∵CP平分∠ACD，
∴∠1=∠3，
∴∠1=∠2（等量代换）．
故答案为：两直线平行，内错角相等，∠3．
点评 本题主要考查了平行线的性质的运用，解题时注意：两直线平行，内错角相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在矩形ABCD中，DC=4$\sqrt{3}$，CF⊥BD分别交BD、AD于点E、F，连接BF．
10．下列各式中，为完全平方式的是（ ）
| A． | x2-6x-9 | B． | x2-6x+9 | C． | 4+2y-y2 | D． | 4y2+2y+1 |
7．
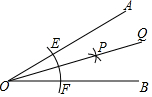观察图中尺规作图的痕迹，下列结论错误的是（ ）
观察图中尺规作图的痕迹，下列结论错误的是（ ）| A． | 射线OP为∠BOA的平分线 | B． | OE=OF | ||
| C． | 点P到OB、OA距离不相等 | D． | 点E、F到OP的距离相等 |
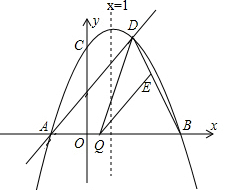已知：如图，二次函数y=ax2+bx+c（a≠0）的图象与y轴交于点C（0，4），与x轴交于点A、B，点B（4，0），抛物线的对称轴为x=1，直线AD交抛物线于点D（2，m）．
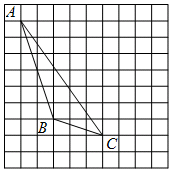如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点．