题目内容
1．设a，b为实数，求2a2+2ab+b2-6a的最小值．分析 原式配方变形后，利用非负数的性质即可求出最小值．
解答 解：原式=（a2+2ab+b2）+a2+6a+9-9
=（a+b）2+（a+3）2-9≥-9，
则当a+b=0，a+3=0，即a=-b=-3时，代数式取得最小值为-9．
点评 此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
12．
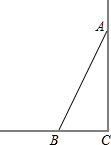如图，一根长为5m的竹竿AB斜靠在竖直的墙壁上，竹竿底端B离墙壁距离3m，则该竹竿的顶端A离地竖直高度为（ ）
如图，一根长为5m的竹竿AB斜靠在竖直的墙壁上，竹竿底端B离墙壁距离3m，则该竹竿的顶端A离地竖直高度为（ ）| A． | 2m | B． | 3m | C． | 4m | D． | $\sqrt{34}$m |
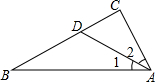如图，∠C=90°，∠1=∠2，AB=15，CD=4，求△ABD的面积．
如图，CD是⊙O的直径，点E在⊙O上，A为DC延长线上一点，连接AE交⊙O于点B，且⊙O得半径为2，若∠EOD=3∠A，求AB的长．