题目内容
6.(1)特殊发现:如图1,若点E,D分别落在边AC,AB上,连接BE,点O为BE的中点,连接OC、OD,试判断线段OC、OD的数量关系以及∠COD、∠ABC的数量关系,并加以证明.
(2)继续探究:
将△ADE绕点A逆时针旋转任意的角度a,请你观察、思考、分析、判断(1)中的结论是否成立.并选取图2证明你的判断.
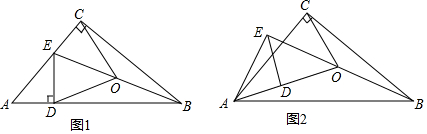
分析 (1)如图1中,结论:OC=OD,∠COD=2∠ABC.利用直角三角形斜边中线的性质即可证明.
(2)如图2中,取AB中点F,连接CD、CF、OF.设∠DAB=∠EAC=α,∠CAD=β.首先证明△EAD∽△BAC,推出$\frac{AD}{AE}$=$\frac{AC}{AB}$,得$\frac{AC}{2OF}$=$\frac{AC}{2CF}$,得$\frac{AD}{OF}$=$\frac{AC}{CF}$,由$\frac{AC}{AD}$=$\frac{FC}{OF}$,∠CFO=∠CAD=β,推出△CFO∽△CAD,再证明△DCO∽△ACF,即可解决问题.
解答 证明:(1)如图1中,结论:OC=OD,∠COD=2∠ABC.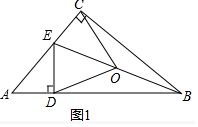
理由:在Rt△ECB中,∵∠ECB=90°.EO=OB,
∴OC=OB=OE,同理可证OD=OB=OE,
∴OC=OD,
∴∠OCB=∠OBC,∠ODB=∠OBD,
∵∠COE=∠OCB+∠OBC,∠EOD=∠ODB+∠OBD,
∴∠COD=∠COE+∠EOD=2∠OBC+2∠OBD=2(∠OBC+∠OBD)=2∠ABC.
(2)结论仍然成立,OC=OD,∠COD=2∠ABC.
理由:如图2中,取AB中点F,连接CD、CF、OF.设∠DAB=∠EAC=α,∠CAD=β.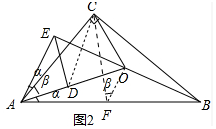
∵∠C=90°,AF=FB,
∴AF=FB=CF,
∴∠AFC=2∠ABC,∠CAF=∠ACF=α+β,
∴∠AFC=180°-2α-2β,
∵OE=OB,AF=FB,
∴FO∥AE,OF=$\frac{1}{2}$AE,
∴∠EAF+∠AFO=180°,
∴(2α+β)+(∠AFC+∠CFO)=180°,
∴2α+β+180°-2α-2β+∠CFO=180°,
∴∠CFO=β=∠CAD,
∵∠EAD=∠BAC,∠ADE=∠ACB=90°,
∴△EAD∽△BAC,
∴$\frac{AD}{AE}$=$\frac{AC}{AB}$,
∴$\frac{AC}{2OF}$=$\frac{AC}{2CF}$,
∴$\frac{AD}{OF}$=$\frac{AC}{CF}$,
∴$\frac{AC}{AD}$=$\frac{FC}{OF}$,∵∠CFO=∠CAD=β,
∴△CFO∽△CAD,
∴∠ACD=∠FCO,$\frac{CF}{CA}$=$\frac{CO}{CD}$,
∴∠DCO=∠ACF,
∴△DCO∽△ACF,
∴∠COD=∠AFC=2∠ABC,$\frac{DO}{AF}$=$\frac{CO}{CF}$
∵△ACF是等腰三角形,
∴FA=FC,
∴OD=OC.∠COD=2∠ABC.
点评 本题考查几何变换综合题、直角三角形斜边中线性质、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加辅助线构造相似三角形解决问题,属于中考压轴题.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
| A. | 点A和点C | B. | 点B和点A | C. | 点C和点B | D. | 点D和点B |
| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
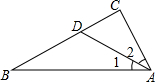 如图,∠C=90°,∠1=∠2,AB=15,CD=4,求△ABD的面积.
如图,∠C=90°,∠1=∠2,AB=15,CD=4,求△ABD的面积.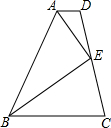 已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD.
已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD.