题目内容
19.定义一种对正整数n的“F”运算:①当n为奇数时,结果为3n+5;
②当n为偶数时,结果为$\frac{n}{2^k}$(其中k是使$\frac{n}{2^k}$为奇数的正整数),并且运算重复进行.
例如,取n=26,那么当n=26时,第2016次“F运算”的结果是62.
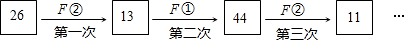
分析 根据新定义规定的运算法则分别计算出第1、2、3、…、11次的运算结果,即可发现从第11次开始,每6次运算为一个周期循环,据此可得.
解答 解:根据题意,得
当n=26时,第1次的计算结果是$\frac{26}{2}$=13,
第2次的计算结果是13×3+5=44,
第3次的计算结果是$\frac{44}{{2}^{2}}$=11,
第4次的计算结果是11×3+5=38,
第5次的计算结果是$\frac{38}{2}$=19,
第6次的计算结果是19×3+5=62,
第7次的计算结果是$\frac{62}{2}$=31,
第8次的计算结果是31×3+5=98,
第9次的计算结果是$\frac{98}{2}$=49,
第10次的计算结果是49×3+5=152,
第11次的计算结果是$\frac{152}{{2}^{3}}$=19,以下每6次运算一循环,
∵(2016-4)÷6=335…2,
∴第2016次“F运算”的结果与第6次的计算结果相同,为62,
故答案为:62.
点评 本题主要考查有理数的混合运算和数字的变化规律,首先要根据题目的要求计算出几个结果,然后利用结果找出规律,最后利用规律即可求出结果.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
7. 如图:∠1=( )度.
如图:∠1=( )度.
 如图:∠1=( )度.
如图:∠1=( )度.| A. | 60 | B. | 80 | C. | 100 | D. | 140 |
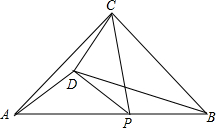 如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.
如图,在等腰直角△ABC中,点P为斜边AB上一动点(不与A、B两点重合),以CP为斜边在直线CP左侧作等腰直角△CPD.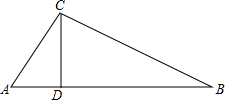 如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.
如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于D,AC=3cm,BC=4cm,AB=5cm.