Question

19．某工厂有许多直角边长分别为30cm和40cm的直角三角形的下脚料铁皮，要利用它们分别裁剪一个正方形，用来焊接棱长为17cm的正方体开关盒．有两种方法：一种是正方形的一边在直角三角形的斜边上，另两个顶点在两条直线边上，如图（1）；另一种是一组邻边在直角三角形的两直角边上，另一个顶点在斜边上，如图（2）．问哪种方式合乎要求．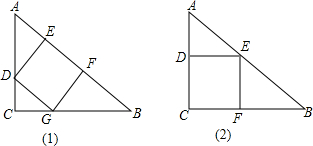

Answer 1

分析 如图（1），利用三角形的面积关系求出AB边上的高，再利用相似三角形的性质求出正方形的边长；
如图（2），设出正方形的边长，再利用相似三角形的性质求出正方形的边长．
边长≥17cm的正方形符合题意．

解答 解：如图（1），因为△ABC为直角三角形，边长分别为30cm和40cm，则AB=$\sqrt{3{0}^{2}+4{0}^{2}}$=50（cm）．
作AB边上的高CH，交DG于点Q．
于是$\frac{2CH}{5}$=$\frac{30×40}{2}$，
故CH=24cm．
易得：△DCG∽△ACB，
故：$\frac{CQ}{CH}$=$\frac{DG}{AB}$．
设正方形DEFG的边长为xcm，
得：$\frac{24-x}{24}$=$\frac{x}{50}$，
解得：x=$\frac{600}{37}$＜17，不合题意，舍去．
如图（2），令AC=3cm，设正方形边长为ycm．
易得：△ADE∽△ACB，
于是：$\frac{AD}{AC}$=$\frac{DE}{CB}$，
$\frac{30-y}{30}$=$\frac{y}{40}$，
解得：y=$\frac{120}{7}$＞17．符合题意．
综上所述，第二种方法合乎要求．

点评 本题考查了相似三角形的应用．（1）利用面积法求出直角三角形斜边上的高是解答此题的关键；（2）可根据△ADE∽△ACB或△BFE∽△BCA来解答．