题目内容
14.用公式法解一元二次方程x2-3x-1=0时,先找出对应的a、b、c,可求得△=13,此方程式的根为x1=$\frac{3+\sqrt{13}}{2}$,x2=$\frac{3-\sqrt{13}}{2}$.分析 找出方程中二次项系数a,一次项系数b及常数项c,计算出根的判别式的值为13大于0,将a,b及c的值代入求根公式即可求出原方程的解.
解答 解:∵a=1,b=-3,c=-1,
∴△=b2-4ac=(-3)2-4×1×(-1)=13,
∴x=$\frac{3±\sqrt{13}}{2}$,
∴原方程的解为x1=$\frac{3+\sqrt{13}}{2}$,x2=$\frac{3-\sqrt{13}}{2}$.
故答案为:13,x1=$\frac{3+\sqrt{13}}{2}$,x2=$\frac{3-\sqrt{13}}{2}$.
点评 此题考查了利用公式法求一元二次方程的解,利用公式法解一元二次方程时,首先将方程化为一般形式,找出二次项系数,一次项系数及常数项,计算出根的判别式,当根的判别式大于等于0时,将a,b及c的值代入求根公式即可求出原方程的解.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 正数与正数的差是正数 | B. | 负数与负数的差是正数 | ||
| C. | 正数减去负数差为正数 | D. | 0减去正数,差为正数 |
4.下列交换加数的位置的变形中,错误的是( )
| A. | 30+(-20)=(-20)+30 | B. | (-5)+(-13)=(-13)+(-5) | C. | (-37)+16=16+(-37) | D. | 10+(-20)=20+(-10) |
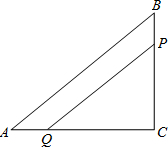 如图,在Rt△ABC中,∠C=90°,AC=7,BC=5,点P从点B开始沿BC以1单位/秒的速度向C点运动,同时点Q从点C开始沿CA以2单位/秒的速度向A点运动(当有一点到达重点时,运动随即停止).
如图,在Rt△ABC中,∠C=90°,AC=7,BC=5,点P从点B开始沿BC以1单位/秒的速度向C点运动,同时点Q从点C开始沿CA以2单位/秒的速度向A点运动(当有一点到达重点时,运动随即停止).