题目内容
14.下列说法正确的是( )| A. | 如果a>b>0,那么$\frac{1}{a}>\frac{1}{b}$ | |
| B. | 函数y=$\frac{{\sqrt{x+1}}}{x}$自变量的取值范围是x≥-1 | |
| C. | 2<$\sqrt{5}$<3 | |
| D. | 若a≠0,则$\frac{{\sqrt{a^2}}}{a}$=1 |
分析 A:根据不等式的性质判断即可;
B:当表达式的分母中含有自变量时,自变量取值要使分母不为零,据此判断即可;
C:由$\sqrt{4}<\sqrt{5}<\sqrt{9}$,可得2<$\sqrt{5}$<3,据此判断即可;
D:分两种情况讨论:(1)a>0时;(2)a<0时,求出$\frac{{\sqrt{a^2}}}{a}$的值是多少即可.
解答 解:∵a>b>0,
∴$\frac{1}{a}<\frac{1}{b}$,
∴选项A错误;
∵函数y=$\frac{{\sqrt{x+1}}}{x}$自变量的取值范围是x≥-1,且x≠0,
∴选项B错误;
∵$\sqrt{4}<\sqrt{5}<\sqrt{9}$,
∴2<$\sqrt{5}$<3,
∴选项C正确;
∵a>0时,$\frac{{\sqrt{a^2}}}{a}$=1,a<0时,$\frac{{\sqrt{a^2}}}{a}$=-1,
∴选项D错误.
故选:C.
点评 (1)此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.
(2)此题还考查了估计无理数的大小,以及二次根式的性质和化简方法,要熟练掌握.
(3)此题还考查了函数自变量的取值范围,要熟练掌握,解答此题的关键是要明确:①当表达式的分母中含有自变量时,自变量取值要使分母不为零.②当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.

练习册系列答案
相关题目
2.只用下列正多边形地砖中的一种,不能镶嵌的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
6.下列各式化成最简二次根式后被开方数是2的是( )
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{24}$ |
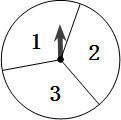 有一个转盘如图所示被平均分成3份,分别标有数字1、2、3,转盘上有一固定指针.转动转盘,当转盘停止时,指针指向哪一个数字即为转出的数字(若指针指向两个扇形的交线时,重新转动转盘).两人进行游戏,一人转动转盘,另一人掷骰子同时按所选方案的规则猜数(骰子的六个面分别标有数字1、2、3、4、5、6).如果猜出的数与所选方案的结果相符,则猜数的人获胜,否则,转盘的人获胜.猜数游戏有下列两种方案:
有一个转盘如图所示被平均分成3份,分别标有数字1、2、3,转盘上有一固定指针.转动转盘,当转盘停止时,指针指向哪一个数字即为转出的数字(若指针指向两个扇形的交线时,重新转动转盘).两人进行游戏,一人转动转盘,另一人掷骰子同时按所选方案的规则猜数(骰子的六个面分别标有数字1、2、3、4、5、6).如果猜出的数与所选方案的结果相符,则猜数的人获胜,否则,转盘的人获胜.猜数游戏有下列两种方案: 背景材料:近年来由于世界各国大力发展海洋经济、加强海洋能力开发,海洋争端也呈上升趋势.为增强海洋执法能力、维护海洋领土,近期我国多个部门联合进行护航、护渔演习.
背景材料:近年来由于世界各国大力发展海洋经济、加强海洋能力开发,海洋争端也呈上升趋势.为增强海洋执法能力、维护海洋领土,近期我国多个部门联合进行护航、护渔演习.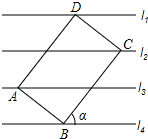 已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=6,BC=8,则tanα的值等于( )
已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为h,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=6,BC=8,则tanα的值等于( )