题目内容
15．已知一组数据a，b，c的平均数为5，方差为4，那么数据a-2，b-2，c-2的平均数和方差分别是（ ）| A． | 3，2 | B． | 3，4 | C． | 5，2 | D． | 5，4 |
分析 根据数据a，b，c的平均数为5可知$\frac{1}{3}$（a+b+c）=5，据此可得出$\frac{1}{3}$（a-2+b-2+c-2）的值；再由方差为4可得出数据a-2，b-2，c-2的方差．
解答 解：∵数据a，b，c的平均数为5，
∴$\frac{1}{3}$（a+b+c）=5，
∴$\frac{1}{3}$（a-2+b-2+c-2）=$\frac{1}{3}$（a+b+c）-2=5-2=3，
∴数据a-2，b-2，c-2的平均数是3；
∵数据a，b，c的方差为4，
∴$\frac{1}{3}$[（a-5）2+（b-5）2+（c-5）2]=4，
∴a-2，b-2，c-2的方差=$\frac{1}{3}$[（a-2-3）2+（b-2-3）2+（c--2-3）2]=$\frac{1}{3}$[（a-5）2+（b-5）2+（c-5）2]=4．
故选B．
点评 本题考查的是方差，熟记方差的定义是解答此题的关键．
练习册系列答案
相关题目
5．已知下列命题：
①各边相等的多边形是正多边形；
②相等的圆心角所对的弧相等；
③若a2=b2，则a=b；
④若直线y=kx+b经过第一、二、四象限，则k＜0，b＞0．
其中原命题与逆命题都是真命题的个数是（ ）
①各边相等的多边形是正多边形；
②相等的圆心角所对的弧相等；
③若a2=b2，则a=b；
④若直线y=kx+b经过第一、二、四象限，则k＜0，b＞0．
其中原命题与逆命题都是真命题的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
正方形A1B1C1O，A2B2C2C1，A3B3C3C2…按如图所示放置，点A1、A2、A3…在直线y=x+1上，点C1、C2、C3…在x轴上，则An的坐标是（2n-1-1，2n-1），．
3．
如图所示的几何体是由五个小正方体组成的，它的左视图是（ ）
如图所示的几何体是由五个小正方体组成的，它的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |
10．
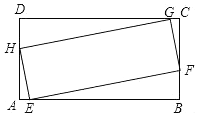如图，四边形EFGH与四边形ABCD均为矩形，点E，F，G，H分别在边AB，BC，CD，DA上，且EF=3HE，AB=2BC，则tan∠AHE=（ ）
如图，四边形EFGH与四边形ABCD均为矩形，点E，F，G，H分别在边AB，BC，CD，DA上，且EF=3HE，AB=2BC，则tan∠AHE=（ ）| A． | $\frac{1}{5}$ | B． | $\frac{1}{6}$ | C． | $\frac{2}{7}$ | D． | $\frac{3}{10}$ |
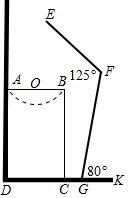如图是小强洗漱时的侧面示意图，洗漱台（矩形ABCD）靠墙摆放，高AD=80cm，宽AB=48cm，小强身高166cm，下半身FG=100cm，洗漱时下半身与地面成80°（∠FGK=80°），身体前倾成125°（∠EFG=125°），脚与洗漱台距离GC=15cm（点D，C，G，K在同一直线上）．