题目内容
5.已知圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积为9πcm2(答案保留π)分析 由于圆锥的高,底面半径,母线构成直角三角形,故圆锥的底面半径可由勾股定理求得,再利用圆锥的底面面积公式计算.
解答 解:由题意知:圆锥的底面半径R=$\sqrt{{5}^{2}-{4}^{2}}$=3,
则圆锥的底面积=πR2=9πcm2,
故答案为:9π.
点评 此题主要考查了圆锥的性质,要知道圆锥的高,底面半径,母线构成直角三角形,解此类题目要根据所构成的直角三角形的勾股定理作为等量关系求解.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
13.某班在体育课上进行1000米测试,在起点处学生小明比小华先跑1分钟,当小明到达终点时,小华还有440米没跑.已知小明每秒钟比小华每秒钟多跑1米.设小华速度为x米/秒,则可列方程为( )
| A. | $\frac{1000}{x+1}$+1=$\frac{1000-440}{x}$ | B. | $\frac{1000}{x+1}$+60=$\frac{1000-440}{x}$ | ||
| C. | $\frac{1000}{x+1}$-1=$\frac{1000-440}{x}$ | D. | $\frac{1000}{x+1}$-60=$\frac{1000-440}{x}$ |
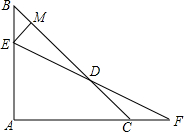 如图,AB=AC,∠A=90°,点E在AB上,点F在AC的延长线上,且BE=CF,EF交直线BC于D,过E点作EM⊥BC,垂足为M,试探究DM与BC之间存在怎样的数量关系?并给予证明.
如图,AB=AC,∠A=90°,点E在AB上,点F在AC的延长线上,且BE=CF,EF交直线BC于D,过E点作EM⊥BC,垂足为M,试探究DM与BC之间存在怎样的数量关系?并给予证明.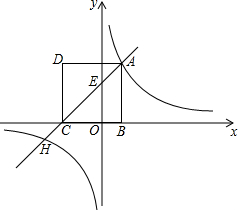 如图,已知四边形ABCD是正方形,边BC在x轴上,点A在反比例函数y=$\frac{4}{x}$的图象上,直线AC与y轴交于点E(0,3),与反比例函数y=$\frac{4}{x}$的图象的另一个交点为H.
如图,已知四边形ABCD是正方形,边BC在x轴上,点A在反比例函数y=$\frac{4}{x}$的图象上,直线AC与y轴交于点E(0,3),与反比例函数y=$\frac{4}{x}$的图象的另一个交点为H. 如图,?ABCD的顶点O为坐标原点,点A在x轴正半轴上,∠COA=60°,OA=10,OC=4,反比例函数的图象在第一象限内过点C.
如图,?ABCD的顶点O为坐标原点,点A在x轴正半轴上,∠COA=60°,OA=10,OC=4,反比例函数的图象在第一象限内过点C.