题目内容
2. 如图,正方形ABCD边长为6,点E、O、Q分别在边AB、AD、CD上,点K、G、N都在对角线AC上,当四边形EBMG和四边形OKNQ都为正方形时,KG的值是$\sqrt{2}$.
如图,正方形ABCD边长为6,点E、O、Q分别在边AB、AD、CD上,点K、G、N都在对角线AC上,当四边形EBMG和四边形OKNQ都为正方形时,KG的值是$\sqrt{2}$.
分析 根据正方形的性质得到∠BAC=∠ACB=45°,∠B=90°,∠BEG=∠BMG=90°,BE=BM=EG=MG,推出△AEG与△CMG是等腰直角三角形,得到AE=EG=CM=GM,根据勾股定理得到AG=$\sqrt{2}$AE,CG=$\sqrt{2}$CM,得到AG=CG=$\frac{1}{2}$AC,同理得到AK=KN=CN=$\frac{1}{3}$AC,于是得到结论.
解答 解:∵四边形ABCD是正方形,
∴∠BAC=∠ACB=45°,∠B=90°,
∵四边形EBMG为正方形,
∴∠BEG=∠BMG=90°,BE=BM=EG=MG,
∴∠AEG=∠CMG=90°,
∴△AEG与△CMG是等腰直角三角形,
∴AE=EG=CM=GM,
∴AG=$\sqrt{2}$AE,CG=$\sqrt{2}$CM,
∴AG=CG=$\frac{1}{2}$AC,
∵正方形ABCD边长为6,
∴AC=6$\sqrt{2}$,
∴AG=CG=3$\sqrt{2}$,
同理△AKO与△CNQ是等腰直角三角形,
∴AK=KN=CN=$\frac{1}{3}$AC,
∴AK=2$\sqrt{2}$,
∴KG=AG-AK=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了正方形的性质,等腰直角三角形的判定和性质,勾股定理,熟练掌握正方形的性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )
如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )
 如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )
如图,这是一个“上”字的造型,其中AB∥CD,∠DCE=80°,则∠BEF等于( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
14.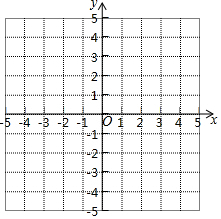 请按要求画出函数y=$\frac{1}{2}$x2的图象:
请按要求画出函数y=$\frac{1}{2}$x2的图象:
(1)列表;
(2)描点;
(3)连线;
(4)请你判断点(4,8)、(-$\frac{1}{2}$,-$\frac{1}{8}$)是否在函数图象上,答:点(4,8)在函数图象上,点(-$\frac{1}{2}$,-$\frac{1}{8}$)不在函数图象上.
 请按要求画出函数y=$\frac{1}{2}$x2的图象:
请按要求画出函数y=$\frac{1}{2}$x2的图象:(1)列表;
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | $\frac{9}{2}$ | 2 | $\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 2 | $\frac{9}{2}$ | … |
(3)连线;
(4)请你判断点(4,8)、(-$\frac{1}{2}$,-$\frac{1}{8}$)是否在函数图象上,答:点(4,8)在函数图象上,点(-$\frac{1}{2}$,-$\frac{1}{8}$)不在函数图象上.
 如图,已知AB∥CD,∠E=∠F,猜想∠1与∠2有怎样的大小关系?并证明你的结论.
如图,已知AB∥CD,∠E=∠F,猜想∠1与∠2有怎样的大小关系?并证明你的结论.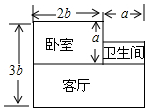 小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖
小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖
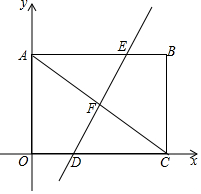 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.