题目内容
7.在一次数学活动中,小辉将一块矩形纸片ABCD对折,使AD与BC重合,得到折痕EF(即EF为AB的垂直平分线),把纸片展开,再将△BAM沿BM折叠,得到△BNM(即△BAM≌△BNM).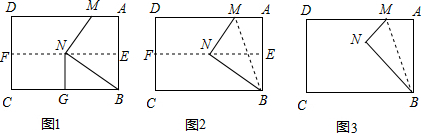
(1)如图1,若点N刚好落在折痕EF上时,且过N作NG⊥BC,求证:NG=$\frac{1}{2}$BN;
(2)如图2,当点N刚好落在折痕EF上时,求∠NBC的度数;
(3)如图3,当M为射线AD上的一个动点时,已知AB=3,BC=5,若△BNC是直角三角形时,请求出AM的长.
分析 (1)根据四边形ABCD为矩形结合折叠的性质得到△ABM≌△GBN,且EF⊥AB,从而得到四边形NGBE为矩形,利用矩形的性质证得NG=$\frac{1}{2}$BN;
(2)连接AN,首先由折叠易知△ABM≌△GBN,且EF⊥AB,E为AB中点,从而证得△BAN为等边三角形,利用等边三角形的性质得到∠NBG=30°即可;
(3)根据四边形ABCD为矩形得到∠A=∠MNB=90°,然后分当∠NBC=90°、当∠BNC=90° N在矩形ABCD内部、当∠BNC=90° N在矩形ABCD外部时三种情况利用勾股定理求得结论即可.
解答 (1)证明:∵四边形ABCD为矩形,
∴∠ABC=90°,
∵NG⊥BC,
∴∠NGB=90°,
由折叠易知△ABM≌△GBN,且EF⊥AB,E为AB中点,
∴∠FEB=90°,AB=BN,
∴四边形NGBE为矩形,
∴BE=NG,
∵BE=$\frac{1}{2}$AB=$\frac{1}{2}$BN,
∴NG=$\frac{1}{2}$BN;
(2)连接AN,
∵由折叠易知△ABM≌△GBN,且EF⊥AB,E为AB中点,
∴AB=BN,NA=BN,
∴△BAN为等边三角形,
∴∠ABN=60°,
∵∠ABC=90°,
∴∠NBG=30°;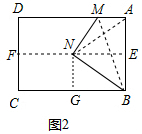
(3)∵四边形ABCD为矩形,
∴∠A=∠MNB=90°,
①当∠NBC=90°,∠NCB=90°都不符合题意,舍去,
②当∠BNC=90°,N在矩形ABCD内部,
∵∠BNC=∠MNB=90°,
∴M、N、C三点共线,
∵AB=BN=3 BC=5∠BNC=90°
∴NC=4
设AM=MN=x
∵MD=5-x,MC=4+x,
∴在Rt△MDC中CD2+MD2=MC2,
32+(5-x)2=(4+x)2,
解得x=1;
③当∠BNC=90° N在矩形ABCD外部时,
∵∠BNC=∠MNB=90°,
∴M、C、N三点共线,
∵AB=BN=3,BC=5,∠BNC=90°,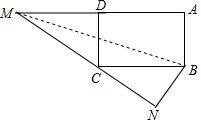 ∴NC=4,
∴NC=4,
设AM=MN=y,
∵MD=y-5,MC=y-4,
∴在Rt△MDC中 CD2+MD2=MC2
32+(y-5)2=(y-4)2,
解得x=9,
综上所述:当AM=1或9时△NBC是直角三角形.
点评 本题考查了四边形的综合知识,解答过程中应用了全等三角形的性质、勾股定理等知识,综合性强,特别是在解答第三问时应用到了分类讨论的数学思想,难度较大,是一道好题.

| x | … | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 0 | -3 | -6 | -6 | -3 | … |
①$\frac{c}{a}$=6;②函数y=ax2+bx+c的最小值为-6;③抛物线的对称轴是x=$\frac{7}{2}$;④方程ax2+bx+c=0有两个正整数解.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
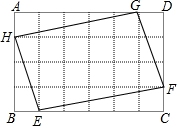 如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )
如图,矩形ABCD是由24个大小相等的正方形组成的,?EFGH的四个顶点分别在BC,CD,AD,AB边上,且是某个小正方形的顶点,若?EFGH的面积为32,则矩形ABCD的面积为( )| A. | 24$\sqrt{2}$ | B. | 12$\sqrt{22}$ | C. | 24 | D. | 48 |
 如图,将长方形ABCD分割成1个灰色长方形与52个边长为1的小正方形,若灰色长方形的长与宽之比为7:5,则灰色长方形的长为14.
如图,将长方形ABCD分割成1个灰色长方形与52个边长为1的小正方形,若灰色长方形的长与宽之比为7:5,则灰色长方形的长为14. 如图,正方形ABCD边长为6,点E、O、Q分别在边AB、AD、CD上,点K、G、N都在对角线AC上,当四边形EBMG和四边形OKNQ都为正方形时,KG的值是$\sqrt{2}$.
如图,正方形ABCD边长为6,点E、O、Q分别在边AB、AD、CD上,点K、G、N都在对角线AC上,当四边形EBMG和四边形OKNQ都为正方形时,KG的值是$\sqrt{2}$.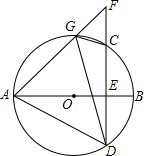 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线交于点F,连接AD,GD,CG.
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线交于点F,连接AD,GD,CG.