题目内容
18.关于x的一元二次方程x2+2x-2m+1=0的两实数根之积为负,则实数m的取值范围是m>$\frac{1}{2}$.分析 设x1、x2为方程x2+2x-2m+1=0的两个实数根.由方程有实数根以及两根之积为负可得出关于m的一元一次不等式组,解不等式组即可得出结论.
解答 解:设x1、x2为方程x2+2x-2m+1=0的两个实数根,
由已知得:$\left\{\begin{array}{l}{△≥0}\\{{x}_{1}•{x}_{2}<0}\end{array}\right.$,即$\left\{\begin{array}{l}{8m≥0}\\{-2m+1<0}\end{array}\right.$
解得:m>$\frac{1}{2}$.
故答案为:m>$\frac{1}{2}$.
点评 本题考查了根与系数的关系、根的判别式以及解一元一次不等式,解题的关键是得出关于m的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据根的情况结合根的判别式以及根与系数的关系得出关于m的一元一次不等式组是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.据统计,某市人口总数为3780000人,用科学记数法表示为( )
| A. | 0.378×107 | B. | 37.8×105 | C. | 3.78×106 | D. | 378×104 |
6.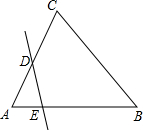 已知直线DE与不等边△ABC的两边AC,AB分别交于点D,E,若∠CAB=60°,则图中∠CDE+∠BED=( )
已知直线DE与不等边△ABC的两边AC,AB分别交于点D,E,若∠CAB=60°,则图中∠CDE+∠BED=( )
 已知直线DE与不等边△ABC的两边AC,AB分别交于点D,E,若∠CAB=60°,则图中∠CDE+∠BED=( )
已知直线DE与不等边△ABC的两边AC,AB分别交于点D,E,若∠CAB=60°,则图中∠CDE+∠BED=( )| A. | 180° | B. | 210° | C. | 240° | D. | 270° |
13.在求3x的倒数的值时,嘉淇同学误将3x看成了8x,她求得的值比正确答案小5.依上述情形,所列关系式成立的是( )
| A. | $\frac{1}{3x}$=$\frac{1}{8x}$-5 | B. | $\frac{1}{3x}$=$\frac{1}{8x}$+5 | C. | $\frac{1}{3x}$=8x-5 | D. | $\frac{1}{3x}$=8x+5 |
7.下列事件中,是必然事件的是( )
| A. | 三条线段可以组成一个三角形 | B. | 400人中有两个人的生日在同一天 | ||
| C. | 早上的太阳从西方升起 | D. | 打开电视机,它正在播放动画片 |
8.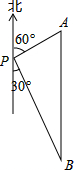 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )| A. | 60海里 | B. | 45海里 | C. | 20$\sqrt{3}$海里 | D. | 30$\sqrt{3}$海里 |
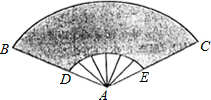 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为30cm,扇面贴纸部分BD的长为20cm.则贴纸部分的面积为$\frac{1000}{3}$πcm2(结果保留π).
如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为30cm,扇面贴纸部分BD的长为20cm.则贴纸部分的面积为$\frac{1000}{3}$πcm2(结果保留π).