题目内容
18.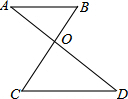 如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,则∠A=45°,∠D=45°.
如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,则∠A=45°,∠D=45°.
分析 先根据三角形外角性质计算出∠A=45°,然后根据平行线的性质得到∠D=∠A=45°.
解答 解:∵∠AOC=∠A+∠B,
而∠AOC=95°,∠B=50°,
∴∠A=95°-50°=45°,
∵AB∥CD,
∴∠D=∠A=45°.
故答案为45°,45°.
点评 本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了三角形外角性质.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
10.正n边形的一个内角与正2n边形的一个内角和等于270°,则n等于( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
7.四边形ABCD中,如果AD∥BC,那么∠A:∠B:∠C:∠D可以等于( )
| A. | 5:1:2:4 | B. | 5:4:2:1 | C. | 5:2:4:1 | D. | 1:2:4:5 |
8.下列图形中不可能是正多边形的是( )
| A. | 三角形 | B. | 正方形 | C. | 四边形 | D. | 梯形 |
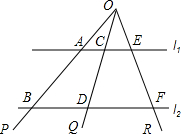 如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.
如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.