题目内容
10．正n边形的一个内角与正2n边形的一个内角和等于270°，则n等于（ ）| A． | 7 | B． | 6 | C． | 5 | D． | 4 |
分析 根据多边形内角和公式可得正n边形的每个内角的度数为：$\frac{180（n-2）}{n}$，正2n边形的每个内角为$\frac{180（2n-2）}{2n}$，根据题意可得方程：$\frac{180（n-2）}{n}$+$\frac{180（2n-2）}{2n}$=270，再解方程即可．
解答 解：由题意得：
$\frac{180（n-2）}{n}$+$\frac{180（2n-2）}{2n}$=270，
解得：n=6，
检验：当n=6时，2n≠0，
故分式方程的解为n=6．
答：n的值为6．
故选：B．
点评 此题主要考查了多边形的内角，关键是掌握多边形的内角和公式．
练习册系列答案
相关题目
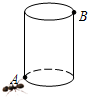如图所示．有一个圆柱．它的高等于12厘米．底面半径等于$\frac{5}{6}$厘米．在圆柱下底面的A点有一只蚂蚁．它想吃到上底面B点处的食物．沿圆柱侧面爬行的最短路程是多少？（π的值取3）．
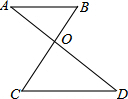如图所示，直线AD和BC相交于点O，AB∥CD，∠AOC=95°，∠B=50°，则∠A=45°，∠D=45°．
如图，在Rt△ABC中，∠C=90°，BD是∠ABC的平分线，∠A=30°，求∠BDC的度数．
如图，∠1=∠2，AD与BE相交于点G，EF∥AD，交BC于点F．试证明：∠BEF=∠ABC．
2．函数y=2x2+4x-5中，当-3≤x＜2时，则y值的取值范围是（ ）
| A． | -3≤y≤1 | B． | -7≤y≤1 | C． | -7≤y≤11 | D． | -7≤y＜11 |