题目内容
9.以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.

分析 (1)根据SAS证明△EAC与△DAB全等,再利用全等三角形的性质解答即可;
(2)利用全等三角形的性质得出∠ECA=∠DBA,进而解答即可;
(3)根据(1)(2)中的证明步骤解答即可.
解答 解:(1)CE=BD,理由如下:
∵等腰Rt△ABC,等腰Rt△ADE,
∴AE=AD,AC=AB,
在△EAC与△DAB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB=90°}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△DAB(SAS),
∴CE=BD;
(2)∵△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECA+∠CBF=∠DBA+∠CBF=45°,
∴∠ECA+∠CBF+∠DCB=45°+45°=90°,
∴∠BFC=180°-90°=90°;
(3)成立,
∵等腰Rt△ABC,等腰Rt△ADE,
∴AE=AD,AC=AB,
在△EAC与△DAB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB=90°}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△DAB(SAS),
∴CE=BD;
∵△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECA+∠CBF=∠DBA+∠CBF=45°,
∴∠ECA+∠CBF+∠DCB=45°+45°=90°,
∴∠BFC=180°-90°=90°.
点评 本题主要考查了全等三角形的判定及其性质、等腰直角三角形的性质,解题的关键是牢固掌握全等三角形的判定及其性质知识点.

练习册系列答案
相关题目
17.用科学记数法记为4.01×104的原数是( )
| A. | 4010 | B. | 40100 | C. | 40.1 | D. | 401000 |
14.甲、乙两名大学生竞选班长,现对甲、乙两名应聘者从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:
(1)如果按笔试占总成绩20%、口试占30%、得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2:1:2来计算各人的成绩,那么又是谁会竞选上?
| 应聘者 | 笔试 | 口试 | 得票 |
| 甲 | 85 | 83 | 90 |
| 乙 | 80 | 85 | 92 |
(2)如果将笔试、口试和得票按2:1:2来计算各人的成绩,那么又是谁会竞选上?
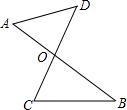 如图,线段AB、CD相交于点O,连接AD、CB.
如图,线段AB、CD相交于点O,连接AD、CB.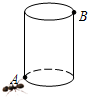 如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).
如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).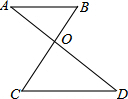 如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,则∠A=45°,∠D=45°.
如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,则∠A=45°,∠D=45°.