题目内容
8.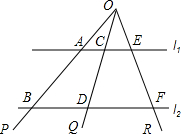 如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.
如图,已知直线l1∥直线l2,直线束(交于同一点的一束直线)OP、OQ、OR截l1、l2,交点分别为A、B、C、D、E、F,求证:AC:CE=BD:DF.
分析 根据平行于三角形一边的直线截其它两边所得三角形与原三角形相似,由AC∥BD得△OAC∽△OBD,由CE∥DF得到△OCE∽△ODF,则利用相似三角形的性质得$\frac{AC}{BD}$=$\frac{OC}{OD}$,$\frac{CE}{DF}$=$\frac{OC}{DF}$,所以$\frac{AC}{BD}$=$\frac{CE}{DF}$,然后利用比例性质即可得到结论.
解答 证明:∵AC∥BD,
∴△OAC∽△OBD,
∴$\frac{AC}{BD}$=$\frac{OC}{OD}$,
∵CE∥DF,
∴△OCE∽△ODF,
∴$\frac{CE}{DF}$=$\frac{OC}{DF}$,
∴$\frac{AC}{BD}$=$\frac{CE}{DF}$,
∴AC:CE=BD:DF.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
17.用科学记数法记为4.01×104的原数是( )
| A. | 4010 | B. | 40100 | C. | 40.1 | D. | 401000 |
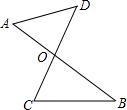 如图,线段AB、CD相交于点O,连接AD、CB.
如图,线段AB、CD相交于点O,连接AD、CB.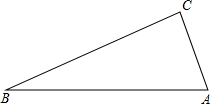 如图,△ABC中,AB=25,AC=7,BC=24,根据题中的已知,提出几个与△ABC有关的问题,并加以解决.
如图,△ABC中,AB=25,AC=7,BC=24,根据题中的已知,提出几个与△ABC有关的问题,并加以解决.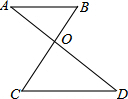 如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,则∠A=45°,∠D=45°.
如图所示,直线AD和BC相交于点O,AB∥CD,∠AOC=95°,∠B=50°,则∠A=45°,∠D=45°.