题目内容
16.在△ABC中,AB,BC,AC三边长分别为$\sqrt{5},\sqrt{10},\sqrt{13}$,求这个三角形的面积.小华同学在解答这题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.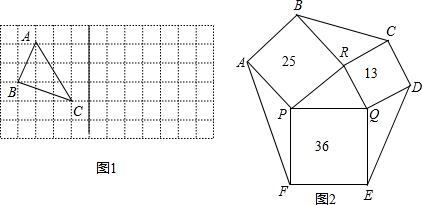
(1)若△DEF三边的长分别为$\sqrt{5}$、$\sqrt{8}$、$\sqrt{17}$,请在正方形网格中画出相应的△DEF,并利用构图法求出它的面积为3(直接写结果);
(2)如图3,一个六边形的花坛被分成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为25cm2,13cm2,36cm2,利用备用图进行构围,计算求出六边形花坛ABCDEF的面积.
分析 (1)根据网格结构和勾股定理作出△DEF,再利用△DEF所在的矩形的面积减去四周三个小直角三角形的面积,计算即可得解;
(2)由构图求出△APF、△DEQ、△PQR、△BCR的面积,总面积等于7个部分的面积之和列式计算即可得解.
解答 解:(1)△DEF如图1所示;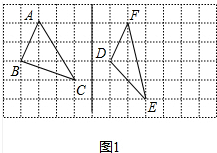
面积=2×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×1×4,
=8-1-2-2,
=8-5,
=3;
(2)构图如图2所示:
∵正方形PRBA、正方形QPFE的面积分别为25cm2,36cm2,
∴正方形PRBA、正方形QPFE的边长分别为5cm、6cm,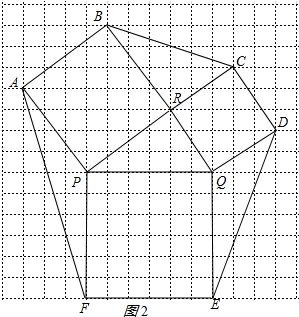
则△APF的面积=$\frac{1}{2}$×6×3=9(cm2),
△DEQ的面积=$\frac{1}{2}$×6×3=9(cm2),
△PQR的面积=$\frac{1}{2}$×6×3=9(cm2),
△BCR的面积=6×4-$\frac{1}{2}$×4×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×6×2=9(cm2),
∴六边形花坛ABCDEF的面积=25+13+36+4×9=74+36=110(cm2).
点评 本题考查了正方形的性质、勾股定理、构图法求三角形的面积;读懂题目信息,理解构图法的操作方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.用一个平面去截正方体,截面不可能是( )
| A. | 七边形 | B. | 六边形 | C. | 五边形 | D. | 四边形 |
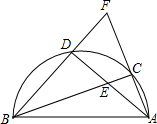 如图,AB是圆的直径,点D是半圆的中点,AC、BD的延长线相交于点F,AD、BC交于点E.求证:DE=DF.
如图,AB是圆的直径,点D是半圆的中点,AC、BD的延长线相交于点F,AD、BC交于点E.求证:DE=DF.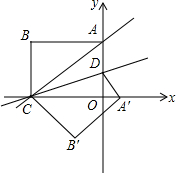 如图,矩形AOCB在直角坐标系中,O为原点,C在x轴上,A在y轴上,直线AC的关系式为y=$\frac{3}{4}$x+9,D是OA上的一点,若将矩形AOCB沿CD折叠,点A恰好落在x轴上的A′处.
如图,矩形AOCB在直角坐标系中,O为原点,C在x轴上,A在y轴上,直线AC的关系式为y=$\frac{3}{4}$x+9,D是OA上的一点,若将矩形AOCB沿CD折叠,点A恰好落在x轴上的A′处.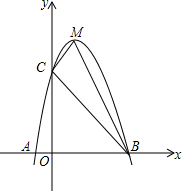 如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).
如图,二次函数y=ax2+bx+c的图象交x轴于A(x1,0),B(x2,0)(x1<x2),交y轴于点C(0,3),其顶点M(1,4).