题目内容
8．已知关于x的方程$\frac{2x+m}{x-1}=3$的解是正数，则m的取值范围为：m＞-3且m≠-2．分析 首先去分母化成整式方程，求得x的值，然后根据方程的解大于0，且x-1≠0即可求得m的范围．
解答 解：去分母，得2x+m=3（x-1），
去括号，得2x+m=3x-3，
解得：x=m+3，
根据题意得：m+3-1≠0且m+3＞0，
解得：m＞-3且m≠-2．
故答案是：m＞-3且m≠-2．
点评 本题考查了分式方程的解，注意到x-1≠0是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．一次足球比赛中，有n（n＞2）个球队参加比赛．假设此次比赛为单循环赛（参加比赛的每一个队都与其他队各赛一场），球队数与总的比赛场数如下表：
当有n个球队参加时，共有多少场比赛？
| 球队数（n） | 2 | 3 | 4 | 5 | 6 |
| 比赛场数 | 1 | 3 | 6 | 10 | 15 |
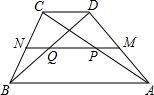梯形ADCB中，AB∥CD，中位线MN与对角线AC，BD分别交于P，Q，设梯形ADCB的周长为L，四边形PDCQ的周长为L1，若AB=2CD，求L1：L的值．
17．一元二次方程2x2-4x+1=0的根的情况是（ ）
| A． | 没有实数根 | B． | 只有一个实数根 | ||
| C． | 有两个相等的实数根 | D． | 有两个不相等的实数根 |