题目内容
 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是考点:二次函数图象与系数的关系
专题:
分析:根据抛物线与y轴的交点在x轴上方得c>0,则可对①进行判断;根据抛物线与x轴有两个交点可对②进行判断;根据抛物线的对称轴为直线x=1,则b=-2a,则可对③进行判断;抛物线与x轴正半轴另一交点坐标为3,所以当-1<x<3时,y>0,x<-1时,y<0,于是可对④进行判断.
解答:解:∵抛物线与y轴的交点在x轴上方,
∴c>0,所以①错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以②正确;
∵抛物线开口向下,
∴a<0;
∵抛物线对称轴为直线x=-
=1,
∴b>0,b=-2a,
∴a+2b=a-4a=-3a>0,所以③错误;
∵对称轴为直线x=1,
∴抛物线与x轴正半轴的交点坐标为3,
∴当x=3时,y=0,
∴-1<x<3时,y>0,
当x<-1时,y<0,
所以④错误.
故答案为②.
∴c>0,所以①错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以②正确;
∵抛物线开口向下,
∴a<0;
∵抛物线对称轴为直线x=-
| b |
| 2a |
∴b>0,b=-2a,
∴a+2b=a-4a=-3a>0,所以③错误;
∵对称轴为直线x=1,
∴抛物线与x轴正半轴的交点坐标为3,
∴当x=3时,y=0,
∴-1<x<3时,y>0,
当x<-1时,y<0,
所以④错误.
故答案为②.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
;抛物线与y轴的交点坐标;当b2-4ac>0,抛物线与x轴有两个交点.
| b |
| 2a |

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
某校2013年给希望工程捐款2万元,以后每年都捐款,计划到2015年三年总共捐款6.62万元,若设该校捐款的年平均增长率为x,则可列方程为( )
| A、2+2x2(1+x)=6.62 |
| B、2(1+x)2=6.62 |
| C、2+2(1+x)+2(1+x)2=6.62 |
| D、2(1+x)3=6.62 |
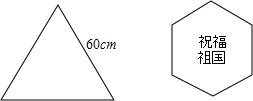 王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )
王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )| A、20cm | B、25cm |
| C、30cm | D、40cm |

 如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.
如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.
 已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积.
已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积. 如图,图中共有线段
如图,图中共有线段 如图,请找出图形的位似中心O.
如图,请找出图形的位似中心O.