题目内容
 已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积.
已知:如图,正方形ABCD的边长我3,点E在BC上,CE=2BE,将正方形折叠,使点A与点E重合,折痕为MN,交AE于点G.求△ANE的面积.考点:正方形的性质,翻折变换(折叠问题)
专题:
分析:设BE=x,则CE=2x,由CE+BE=3得到BE=1,CE=2,由折叠可知AN=NE,那么利用勾股定理可求得BN长,进而求得AN.S△ANE=
AN•BE.
| 1 |
| 2 |
解答:解:设BE=x,则CE=2x,
∵BC=CE+BE=3,
即2x+x=3,x=1,
即设BN=k,则AN=NE=3-k,
由勾股定理得:(3-k)2=k2+12,
解得k=
,
∴AN=3-k=
,
S△ANE=
AN•BE=
×
×1=
.
∵BC=CE+BE=3,
即2x+x=3,x=1,
即设BN=k,则AN=NE=3-k,
由勾股定理得:(3-k)2=k2+12,
解得k=
| 4 |
| 3 |
∴AN=3-k=
| 5 |
| 3 |
S△ANE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| 5 |
| 6 |
点评:本题考查了翻折变换,翻折前后对应边相等,翻折中较复杂的计算,需找到翻折后相应的直角三角形,利用勾股定理求解所需线段.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
如果单项式
x3ya与xby4是同类项,那么(-a)b的值是( )
| 2 |
| 3 |
| A、64 | B、-64 |
| C、81 | D、-81 |
 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是
二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x<3时,y>0.正确的是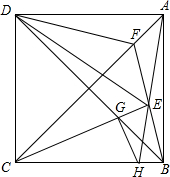 如图,正方形ABCD,以CD为边向正方形内作等边△CDE,连BE交AC于F,连DB交CE与G,连AE并延长交BC于H,连DF,GH.
如图,正方形ABCD,以CD为边向正方形内作等边△CDE,连BE交AC于F,连DB交CE与G,连AE并延长交BC于H,连DF,GH.