题目内容
4.已知△ABC中,三边记为a,b,c.若a2+b2=nc2(n为正整数),则称△ABC为n阶三角形.显然等腰Rt△为1阶三角形,或者为3阶三角形.(1)试判断正三角形的阶数;
(2)若一直角三角形为2阶三角形,求此三角形的三边之比;
(3)反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交矩形ABCO两边所在直线AB,BC于点E,F,点B(2,1),若△OEF为4阶三角形,求k的值.
分析 (1)由△ABC是正三角形,得出a=b=c,得出a2+b2=2c2,b2+c2=2a2,a2+c2=2b2,即可得出结论;
(2)由勾股定理得出a2+b2=c2,再由已知条件得出c2+a2=2b2,证出2a2+b2=2b2,得出b=$\sqrt{2}$a,c=$\sqrt{3}$a,即可得出结论;
(3)根据题意得出F(k,1),E(2,$\frac{k}{2}$),由矩形的性质和勾股定理得出OF2=1+k2,OE2=4+$\frac{{k}^{2}}{4}$,EF2=BF2+BE2=$\frac{5}{4}{k}^{2}$-5k+5;分三种情况:①当OF2+OE2=4EF2时;②当OF2+EF2=4OE2时;③当OE2+EF2=4OF2时;分别得出关于k的方程,解方程即可.
解答 解:(1)正三角形是2阶三角形;理由如下:
∵△ABC是正三角形,
∴a=b=c,
∴a2+b2=2c2,b2+c2=2a2,a2+c2=2b2,
∴正三角形是2阶三角形;
(2)∵△ABC为2阶直角三角形,
∴a2+b2=c2,且c2+a2=2b2,
∴2a2+b2=2b2,
∴b=$\sqrt{2}$a,
∴c=$\sqrt{3}$a,
∴a:b:c=1:$\sqrt{2}$:$\sqrt{3}$;
(3)如图所示: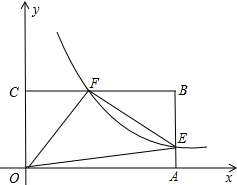 根据题意得:F(k,1),E(2,$\frac{k}{2}$),
根据题意得:F(k,1),E(2,$\frac{k}{2}$),
∵四边形ABCO是矩形,
∴∠OCF=∠B=∠OAB=90°,
∴OF2=1+k2,OE2=4+$\frac{{k}^{2}}{4}$,EF2=BF2+BE2=(2-k)2+(1-$\frac{k}{2}$)2=$\frac{5}{4}{k}^{2}$-5k+5;
分三种情况:①当OF2+OE2=4EF2时,1+k2+4+$\frac{{k}^{2}}{4}$=4($\frac{5}{4}{k}^{2}$-5k+5),
解得:k=$\frac{8±2\sqrt{7}}{3}$;
②当OF2+EF2=4OE2时,1+k2+$\frac{5}{4}{k}^{2}$-5k+5=4(4+$\frac{{k}^{2}}{4}$),
解得:k=2±2$\sqrt{3}$(负值舍去),
∴k=2+2$\sqrt{3}$;
③当OE2+EF2=4OF2时,4+$\frac{{k}^{2}}{4}$+$\frac{5}{4}{k}^{2}$-5k+5=4(1+k2),
解得:k=-1±$\sqrt{3}$(负值舍去),
∴k=-1+$\sqrt{3}$;
综上所述:k的值为$\frac{8±2\sqrt{7}}{3}$,或2+2$\sqrt{3}$,或-1+$\sqrt{3}$.
点评 本题是反比例函数综合题目,考查了正三角形的性质、坐标与图形性质、勾股定理、矩形的性质、一元二次方程的解法以及n阶三角形的定义等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,根据勾股定理列出方程,解方程才能得出结果.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | A | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | B | 1 |
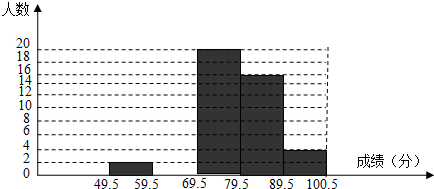
(1)频数、频率分布表中a=8,b=0.08;(答案直接填在题中横线上 )
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
 如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=50°,则∠2=( )
如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=50°,则∠2=( )| A. | 40° | B. | 50° | C. | 60° | D. | 130° |

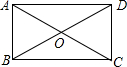 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.