题目内容
9．在一个口袋中有4个完全相同的小球，把它们分别标号为1、2、3、4，随机摸取一个小球然后放回，再随机摸取一个小球，两次摸出小球的标号和等于6的概率是$\frac{3}{16}$．分析 列举出所有情况，看两次摸出的小球的标号的和等于6的情况数占总情况数的多少即可．
解答 解：
共16种情况，和为6的情况数有3种，所以概率为$\frac{3}{16}$．
故答案为：$\frac{3}{16}$．
点评 考查概率的求法；用到的知识点为：概率=所求情况数与总情况数之比．正确的列表或树状图是解答本题的关键，难度不大．
练习册系列答案
相关题目
19．下列计算正确的是（ ）
| A． | （-2a）2=2a2 | B． | a6÷a3=a2 | C． | 3a•a2=3a3 | D． | （-2a2）•（-3a3）=6a6 |
20．
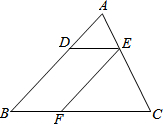如图，已知在△ABC中，点D，E，F分别是边AB，AC，BC上的点，DE∥BC，EF∥AB，且AD：DB=4：7，那么CF：CB等于（ ）
如图，已知在△ABC中，点D，E，F分别是边AB，AC，BC上的点，DE∥BC，EF∥AB，且AD：DB=4：7，那么CF：CB等于（ ）| A． | 7：11 | B． | 4：8 | C． | 4：7 | D． | 3：7 |
14．
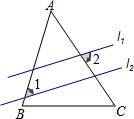如图，直线l1∥l2，且分别与△ABC的两边AB、AC相交，若∠A=55°，∠1=45°，则∠2的度数为（ ）
如图，直线l1∥l2，且分别与△ABC的两边AB、AC相交，若∠A=55°，∠1=45°，则∠2的度数为（ ）| A． | 45° | B． | 55° | C． | 80° | D． | 100° |
1．
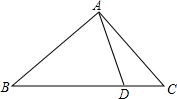如图，D是△ABC一边BC上一点，连接AD，使△ABC∽△DBA的条件是（ ）
如图，D是△ABC一边BC上一点，连接AD，使△ABC∽△DBA的条件是（ ）| A． | AC：BC=AD：BD | B． | AC：BC=AB：AD | C． | AB2=CD•BC | D． | AB2=BD•BC |
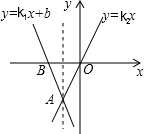如图，直线y=k1x+b经过点A（-1，-2）和点B（-2，0），直线y=k2x经过点A，则二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$，不等式k2x＜k1x+b＜0的解集为x＜-1．